Cho hình vuông ABCD có B(0;4) ; M,N lần lượt là trung điểm BC,CD . Xác định tọa độ các đỉnh hình vuông biết E(5;3) thuộc đường thẳng AM, điểm N thuộc đường thẳng d:x-2y-6=0 và N có tung độ âm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do ABCD là hình vuông \(\Rightarrow AB=d\left(A;BC\right)=\dfrac{\left|0-2.2-1\right|}{\sqrt{1^2+\left(-2\right)^2}}=\sqrt{5}\)
\(\Rightarrow AC=AB\sqrt{2}=\sqrt{10}\)
Do C thuộc BC \(\Rightarrow C\left(2c+1;c\right)\) \(\Rightarrow\overrightarrow{AC}=\left(2c+1;c-2\right)\)
\(\Rightarrow AC^2=\left(2c+1\right)^2+\left(c-2\right)^2=10\)
\(\Leftrightarrow5c^2-5=0\Rightarrow\left[{}\begin{matrix}c=1\\c=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}C\left(3;1\right)\\C\left(-1;-1\right)\end{matrix}\right.\)
Do C có hoành độ dương \(\Rightarrow C\left(3;1\right)\)
N là trung điểm AC \(\Rightarrow N\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)

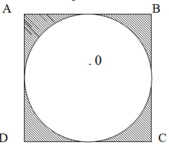
`a)` Vì `5xx5=25` nên cạnh hình vuông bằng `5 cm`
Bán kính hình tròn là: `5:2=2,5(cm)`
Diện tích hình tròn là: `2,5xx2,5xx3,14=19,625(cm^2)`
`b)` Vì `2\sqrt{3}xx2\sqrt{3}=12` nên cạnh hình vuông bằng `2\sqrt{2} cm`
Bán kính hình tròn là: `2\sqrt{3}:2=\sqrt{3})(cm)`
Diện tích hình tròn là: `\sqrt{3}xx\sqrt{3}xx3,14=9,42(cm^2)`
Diện tích phần gạch chéo là: `12-9,42=2,58(cm^2)`



Để giải bài toán này, ta thực hiện các bước sau đây:
Bước 1: Tìm tọa độ của điểm A. Vì hình vuông ABCD là hình vuông nên ta có AB=BC=CD=DA. Vậy, ta có tọa độ điểm A là A(0;6).
Bước 2: Tìm tọa độ của điểm C. Vì M là trung điểm của BC và BM=MC nên ta có tọa độ điểm C là C(2;2).
Bước 3: Tìm tọa độ của điểm D. Vì hình vuông ABCD là hình vuông nên ta có AD vuông góc AB và AD=AB. Vậy, tọa độ điểm D là D(-6;4).
Bước 4: Tìm tọa độ của điểm N. Điểm N có tung độ âm nên nằm dưới trục hoành. Ta cần tìm tọa độ của điểm N bằng cách giải hệ phương trình hợp là của đường thẳng d:x-2y-6=0 và đường thẳng CD: y = -x + 4.
Giải hệ phương trình ta có:
x - 2y = -6y = -x + 4Thay y của phương trình 2 vào phương trình 1 ta có:
x - 2(-x + 4) = -6 <=> x = 2Thay x = 2 vào phương trình 2 ta có: y = -2 + 4 <=> y = 2
Vậy, tọa đó điểm N là N(2;2).
Bước 5: Tìm tọa độ của điểm B. Vì B là đỉnh của hình vuông ABCD và biết tọa độ của điểm A và C nên ta có tọa độ điểm B là B(-2;6).
Bước 6: Tìm tọa độ của điểm E. Ta biết E thuộc đường thẳng AM nên ta có phương trình đường thẳng AM. Ta có tam giác AEM vuông tại E với AM là đường cao. Vậy, ta sử dụng định lý Pythagoras để tìm tọa độ của E.
Đường thẳng AM có hệ số góc bằng: m = (y_A-y_M)/(x_A-x_M) = (6-3)/(0-2) = -1.5
Vậy, phương trình đường thẳng AM là: y = -1.5x + 6 Điểm E thuộc đường thẳng AM nên thay x của E vào phương trình đường thẳng AM ta có: 3 = -1.5x + 6 <=> x = 2
Thay x của E vào phương thức đường thẳng AM ta có: y = -1.5*2 + 6 <=> y = 3
Vậy, tọa độ điểm E là E(2;3).
Bước 7: Tóm tắt kết quả. Tọa độ các đỉnh hình vuông là: A(0;6), B(-2;6), C(2;2), D(-6;4) Đường thẳng AM có phương trình là: y = -1.5x + 6 Tọa độ của điểm E là E(2;3) Điểm N có tọa độ là N(2;2)