Viết phương trình đường thẳng d đi qua điểm A(-4;-5;3) và cắt cả hai đường thẳng d 1 : x + 1 3 + y + 3 - 2 = z - 2 - 1 và d 2 : x - 2 2 = y + 1 3 = z - 1 - 5
![]()
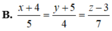
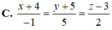
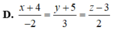
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



5:
Gọi (d): y=ax+b là phương trình cần tìm
Theo đề, ta có hệ:
3a+b=-1 và 2a+b=3
=>a=-4 và b=11
=>y=-4x+11
4:
vecto BC=(1;-1)
=>AH có VTPT là (1;-1)
Phương trình AH là:
1(x-1)+(-1)(y+3)=0
=>x-1-y-3=0
=>x-y-4=0

a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6

a) Vì (d): y=ax+b//y=3x+1 nên \(\left\{{}\begin{matrix}a=3\\b\ne1\end{matrix}\right.\)
Suy ra: (d): y=3x+b
Thay x=2 và y=-2 vào (d), ta được:
\(3\cdot2+b=-2\)
\(\Leftrightarrow b=-8\)(thỏa ĐK)
Vậy: (d): y=3x-8
b) Để (d) vuông góc với y=2x+3 nên \(2a=-1\)
hay \(a=-\dfrac{1}{2}\)
Vậy: (d): \(y=\dfrac{-1}{2}x+b\)
Thay x=-3 và y=4 vào (d), ta được:
\(\dfrac{-1}{2}\cdot\left(-3\right)+b=4\)
\(\Leftrightarrow b+\dfrac{3}{2}=4\)
hay \(b=\dfrac{5}{2}\)
Vậy: (d): \(y=\dfrac{-1}{2}x+\dfrac{5}{2}\)

Gọi đường thẳng đi qua A là d'.
a) Ta có: \(d'\perp d.\)
\(\Rightarrow\) VTPT của d là VTCP của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\overrightarrow{u_{d'}}=\left(3;-4\right).\Rightarrow\overrightarrow{n_{d'}}=\left(4;3\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(4\left(x-2\right)+3\left(y+1\right)=0.\\ \Leftrightarrow4x+3y-5=0.\)
b) Ta có: \(d'//d.\)
\(\Rightarrow\) VTPT của d là VTPT của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\) \(\overrightarrow{n_{d'}}=\left(3;-4\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(3\left(x-2\right)-4\left(y+1\right)=0.\\ \Leftrightarrow3x-4y-10=0.\)

a: Gọi phương trình đường thẳng cần tìm là (d): y=ax+b(a<>0)
Vì (d)//y=3x+2 nên \(\left\{{}\begin{matrix}a=3\\b\ne2\end{matrix}\right.\)
Vậy: (d): y=3x+b
Thay x=1 và y=2 vào (d), ta được:
\(b+3\cdot1=2\)
=>b+3=2
=>b=-1
vậy: (d): y=3x-1
b: Gọi phương trình đường thẳng cần tìm là (d): y=ax+b(a<>0)
Vì (d) có tung độ gốc là 3 nên b=3
=>(d): y=ax+3
Thay x=-4 và y=7 vào (d), ta được:
\(-4a+3=7\)
=>-4a=4
=>a=-1
vậy: (d): y=-x+3
c: A(1;4); B(4;8)
=>\(AB=\sqrt{\left(4-1\right)^2+\left(8-4\right)^2}\)
=>\(AB=\sqrt{3^2+4^2}=\sqrt{25}=5\)
c: y=2x-6
=>2x-y-6=0
Khoảng cách từ A(-3;2) đến đường thẳng 2x-y-6=0 là;
\(d\left(A;2x-y-6=0\right)=\dfrac{\left|\left(-3\right)\cdot2+2\left(-1\right)-6\right|}{\sqrt{2^2+\left(-1\right)^2}}\)
\(=\dfrac{\left|-6-2-6\right|}{\sqrt{5}}=\dfrac{14}{\sqrt{5}}\)

Gọi phương trình đường thẳng d cần tìm là y = a x + b ( a ≠ 0 )
Thay tọa độ điểm A vào phương trình đường thẳng d ta được 3 a + b = 3 ⇒ b = 3 – 3 a
Thay tọa độ điểm B vào phương trình đường thẳng d ta được − 1 . a + b = 4 ⇒ b = 4 + a
Suy ra 3 − 3 a = 4 + a ⇔ 4 a = − 1 ⇔ a = − 1 4 ⇒ b = 4 + a = 4 + 1 4
= 15 4 ⇒ y = − 1 4 x + 15 4
Vậy d: y = − 1 4 x + 15 4
Đáp án cần chọn là: B

a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+3=-3x-2\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)

\(a,\text{PT hoành độ giao điểm: }2x+3=-3x-2\Leftrightarrow x=-1\Leftrightarrow y=1\Leftrightarrow A\left(-1;1\right)\\ b,\text{Gọi đt đó là }y=ax+b\\ \Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\a=-1;b\ne5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\Leftrightarrow y=-x\\ d,\text{Gọi đt cần tìm là }y=ax+b\\ \Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\Leftrightarrow y=-2x-1\)

a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+3=-3x-2\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)