Tìm số giá trị nguyên thuộc đoạn [-209;2019] của tham số m để đồ thị hàm số y = x - 3 x 2 + x - m có đúng hai đường tiệm cận
A. 2007
B. 2010
C. 2009
D. 2008
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
2 tháng 10 2019
Đúng(0)
Những câu hỏi liên quan
CM
30 tháng 4 2018
Đặt t = log 3 2 x + 1 . Do 1 ≤ x ≤ 3 3 nên 1 ≤ t ≤ 2
Phương trình đã cho có ít nhất một nghiệm thuộc đoạn 1 ; 3 3
⇔ Phương trình t 2 - 1 + t - 2 m - 1 = 0 có ít nhất một nghiệm thuộc đoạn [ 1;2 ]
⇔ Phương trình t 2 + t - 2 = 2 m có ít nhất một nghiệm thuộc đoạn [ 1;2 ]
Xét hàm số f t = t 2 + t - 2 , t ∈ 1 ; 2
f ' t = 2 t + 1 > 0 , ∀ t ∈ 1 ; 2 ⇒ là hàm đồng biến trên [ 1;2 ] ⇒ f 1 ≤ f t ≤ f 2 ⇔ 0 ≤ m ≤ 2
Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán
Đáp án C
CM
13 tháng 3 2017
Chọn D.
Phương pháp:
+) Đường thẳng x = a được gọi là TCĐ của đồ thị hàm số
Đồ thị hàm số chỉ có đúng 2 đường tiệm cận ⇔ đồ thị hàm số có đúng 1 tiệm cận đứng.
Như vậy có: 2008 giá trị m thỏa mãn bài toán.
20 tháng 7 2016
Ta có \(3x^3+13x^2-7x+5\)
= \(3x^3-2x^2+15x^2-10x+3x-2+7\)
= \(x^2\left(3x-2\right)+5x\left(3x-2\right)+\left(3x-2\right)+7\)
= \(\left(3x-2\right)\left(x^2+5x+1\right)+7\)
=> biểu thức ban đầu = \(x^2+5x+1+\frac{7}{3x-2}\)
Vì x nguyên nên x2 + 5x +1 nguyên
=> Để biểu thức nguyên thì 3x - 2 phải là ước của 7
Sau đó bạn tự giải tiếp nhé
Chúc bạn làm bài tốt
11 tháng 8 2016
mk giải câu a thui nha
để \(\frac{6n-1}{3n+2}\)là số nguyên thì:
(6n-1) sẽ phải chia hết cho(3n+2)
mà (3n+2) chja hết cho (3n+2)
=> 2(3n+2) cx sẽ chia hết cho (3n+2)
<=> (6n+4) chia hết cho (3n+2)
mà (6n-1) chia hết cho (3n+2)
=> [(6n+4)-(6n-1)] chja hết cho (3n+2)
(6n+4-6n+1) chja hết cho 3n+2
5 chia hết cho3n+2
=> 3n+2 \(\in\){1,5,-1,-5}
ta có bảng
3n+2 | 1 | 5 | -1 | -5 |
3n | 3 | 7 | 1 | -3 |
| n | 1 | -1 |
vậy....
22 tháng 3 2016
bạn có thể giải thích ra được không !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
BH
0
CM
21 tháng 2 2019
Chọn B
Xét g(x) = x 4 - 4 x 3 + 4 x 2 + a với x ∈ [0;2]
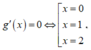
Bảng biến thiên g(x)
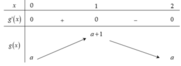
Trường hợp 1: a ≥ 0. Khi đó M = a + 1; m = a
Ta có M
≤
2m 
Với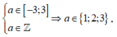 
Trường hợp 2: 
Khi đó M = -a; m = -(a+1)
Trường hợp 3: -1 < a < 0. Với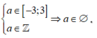 
Vậy có 5 giá trị a cần tìm.