Cho a,b,c là các số thuộc đoạn [ -1;2 ] thõa mãn \(a^2+b^2+c^2=6.\) CMR : \(a+b+c>0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a\left(b-1\right)+b\left(1-c\right)+c\left(1-a\right)\le1\\ \Leftrightarrow-abc+ab+bc+ca-a-b-c+1\le2-abc\\ \Leftrightarrow\left(1-a\right)\left(1-b\right)\left(1-c\right)\le2-abc\)
lại có \(abc\le1\) nên \(2-abc\ge1\)
ta chứng minh \(\left(1-a\right)\left(1-b\right)\left(1-c\right)\le1\)
luôn đúng do \(0\le a;b;c\le1\)
vậy bđt dc cm
tick mik nhaaaaa.mik ms l9 thui

Không mất tính tổng quát, giả sử \(a\ge b\ge c\).
Khi đó: \(\left(a-b\right)\left(b-c\right)\ge0\)
\(\Leftrightarrow ab+bc\ge ac+b^2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{c}+1\ge\dfrac{a}{b}+\dfrac{b}{c}\\\dfrac{c}{a}+1\ge\dfrac{c}{b}+\dfrac{b}{a}\end{matrix}\right.\)
\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}+\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}\le2+2\left(\dfrac{a}{c}+\dfrac{c}{a}\right)\)
Vì \(1\le c\le a\le2\Rightarrow\left(\dfrac{a}{c}-2\right)\left(\dfrac{2a}{c}-1\right)\le0\)
\(\Leftrightarrow\dfrac{a}{c}+\dfrac{c}{a}\le\dfrac{5}{2}\)
\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}+\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}\le7\)
\(\Leftrightarrow\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\le10\)
Đẳng thức xảy ra khi \(a=b=2;c=1\) và các hoán vị.

chứng minh:(a+b+c)(1/a+1/b+1/c)<=10 nha mn. nhanh hộ mình
Không mất tính tổng quát giả sử a≥b≥c\(\Rightarrow \left ( a-b \right )\left ( b-c \right )\geq 0\)
\(\Rightarrow ab+bc\geq b^{2}+ac\)
=>\(\frac{a}{c}+1\geq \frac{b}{c}+\frac{a}{b}\) ; \(\frac{c}{a}+1\geq \frac{b}{a}+\frac{c}{b}\)
=>\(\frac{a}{b}+\frac{b}{c}+\frac{c}{b}+\frac{b}{a}\leq \frac{a}{c}+\frac{c}{a}+2=>\frac{a}{b}+\frac{b}{c}+\frac{c}{a}+\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\leq 2+2(\frac{a}{c}+\frac{c}{a})\)
Đặt \(x=\frac{a}{c},\)ta có 2 >= x >= 1 nên x + 1 /x <=5/2 => \(2 + 2 ( a/c + c/a)\)<= 7 => \(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}+\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\)<=7 => đpcm

Đáp án C
Nhận xét, với x ∈ 1 ; 2 thì f x = x − log 2 x ≤ 0 . Thật vậy, xét f ' x = x ln 2 − 1 x ln 2
→ f ' x = 0 ⇔ x = 1 ln 2 ⇒ max 1 ; 2 f x = max f 1 , f 1 ln 2 , f 2 = 0
Từ đây suy ra x − 1 ≤ log 2 x ⇒ log 2 3 x ≥ x − 1 3 với 1 ; 2 ⇒ 1 ≥ a − 1 3 + b − 1 3 + c − 1 3
Mặt khác cũng có x 3 − 3 x log 2 x ≤ x 3 − 3 x 1 − x = x 3 − 3 x 2 + 3 x với 1 ; 2
⇒ P − 3 ≤ x − 1 3 + y − 1 3 + z − 1 3 = 1 ⇒ P ≤ 4

Đáp án C
Nhận xét, với x ∈ [1;2] thì f(x) = x - log2x ≤ 0. Thật vậy, xét f ' ( x ) = x ln 2 - 1 x ln 2

Từ đây suy ra
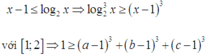
Mặt khác cũng có
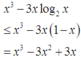
với [1;2]
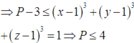

Không mất tính tổng quát, giả sử \(a\ge b\ge c\)
\(\Rightarrow P\le\dfrac{a}{b+c+1}+\dfrac{b}{b+c+1}+\dfrac{c}{b+c+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)\)
\(\Rightarrow P\le\dfrac{a+b+c}{b+c+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)=\dfrac{a-1}{b+c+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)+1\)
\(\Rightarrow P\le\left(1-a\right)\left[\left(1-b\right)\left(1-c\right)-\dfrac{1}{b+c+1}\right]+1\le\left(1-a\right)\left[\left(1-b\right)\left(1-c\right)-\dfrac{1}{bc+b+c+1}\right]+1\)
\(\Rightarrow P\le\left(1-a\right)\left[\left(1-b\right)\left(1-c\right)-\dfrac{1}{\left(1+b\right)\left(1+c\right)}\right]+1\)
\(\Rightarrow P\le\left(1-a\right)\left(\dfrac{\left(1-b^2\right)\left(1-c^2\right)-1}{\left(1+b\right)\left(1+c\right)}\right)+1\)
Do \(a;b;c\le1\Rightarrow\left\{{}\begin{matrix}1-a\ge0\\\left(1-b^2\right)\left(1-c^2\right)\le1\\\end{matrix}\right.\) \(\Rightarrow\left(1-a\right)\left[\dfrac{\left(1-b^2\right)\left(1-c^2\right)-1}{\left(1+b\right)\left(1+c\right)}\right]\le0\)
\(\Rightarrow P\le1\)
\(P_{max}=1\) khi \(\left(a;b;c\right)=\left(0;0;0\right);\left(1;1;1\right);\left(0;1;1\right);\left(0;0;1\right)\) và các hoán vị
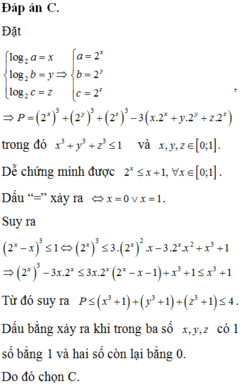
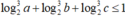 . Khi biểu thức
. Khi biểu thức 



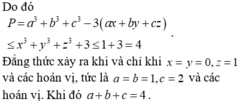
\(-1\le a;b;c\le2\)
\(\Rightarrow\left(a+1\right)\left(a-2\right)\le0\)
\(\Leftrightarrow a^2-a-2\le0\)
\(\Rightarrow a^2-2\le a\)
Tương tự ta có: \(b^2-2\le b\) ; \(c^2-2\le c\)
\(\Rightarrow a+b+c\ge a^2+b^2+c^2-6=0\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(-1;-1;2\right)\) và cách hoán vị