Cho điểm M(1;2) và cho 2 đường thẳng \(d_1=\frac{x-3}{3}=\frac{y}{-1}\); \(d_2:\begin{cases}x=3+t\\y=-2t\end{cases}\) \(t\in R\)
Viết phương trình đường thẳng \(\Delta\) đi qua M cắt lần lượt \(d_1,d_2\) tại A, B sao cho M là trung điểm của đoạn AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 6 2017
Đáp án B
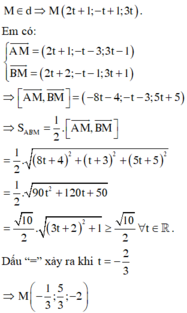
Đường thẳng AB: qua A 0 ; 4 ; 1 vtcp u → = AB → = − 1 ; − 2 ; − 2 ⇒ AB : x = t y = 4 + 2 t z = 1 + 2 t
Gọi H là hình chiếu vuông góc của điểm M trên đường thẳng AB.
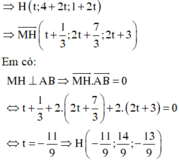
H là trung điểm của MM’ nên M ' − 19 9 ; 13 9 ; − 8 9 .
Vậy tổng tọa độ của điểm M’ là: − 14 9 .
30 tháng 11 2023
Bài 1:
\(y=\left(m-1\right)x^2+2mx-3m+1\)
\(=mx^2-x^2+2mx-3m+1\)
\(=m\left(x^2+2x-3\right)-x^2+1\)
Tọa độ điểm cố định mà (Pm) luôn đi qua là:
\(\left\{{}\begin{matrix}x^2+2x-3=0\\y=-x^2+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+3\right)\left(x-1\right)=0\\y=-x^2+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\\y=-x^2+1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3=0\\y=-x^2+1\end{matrix}\right.\\\left\{{}\begin{matrix}x-1=0\\y=-x^2+1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-3\\y=-\left(-3\right)^2+1=-9+1=-8\end{matrix}\right.\\\left\{{}\begin{matrix}x=1\\y=-1^2+1=0\end{matrix}\right.\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2024
Theo công thức trung điểm:
\(\left\{{}\begin{matrix}x_M=2x_B-x_A=5\\y_M=2y_B-y_A=6\end{matrix}\right.\) \(\Rightarrow M\left(5;6\right)\)
6 tháng 1 2024
Để B là trung điểm của đoạn thẳng AM, ta cần tìm tọa độ của điểm M.
Theo định nghĩa, trung điểm của một đoạn thẳng là điểm nằm ở giữa hai đầu mút của đoạn đó. Ta áp dụng công thức trung điểm để tìm tọa độ của M.
Công thức trung điểm: M(xM, yM) là trung điểm của đoạn AB <=> (xM, yM) = ((xA + xB)/2, (yA + yB)/2).
Ứng với A(1; -2) và B(3; 2): xM = (1 + 3)/2 = 2, yM = (-2 + 2)/2 = 0.
Vậy tọa độ của điểm M là M(2; 0).
Đáp án đúng là: B. M(2; 0).
CM
25 tháng 12 2018
Chọn C.
Với M(a, b,c) thì điểm đối xứng của M qua mặt phẳng (Oxy) là M’(a;b;- c).
Do đó, điểm đối xứng với điểm M(3;2;-1) qua mặt phẳng (Oxy) là M’(3;2;1).
Xét điểm \(B\left(3+t;-2t\right)\in d_2\). Lấy điểm A sao cho M(1;2) là trung điểm của AB. Khi đó \(A\left(1-t;4+2t\right)\) và
\(A\in d_1\Leftrightarrow\frac{1-t-3}{3}=\frac{4+2t}{-1}\Leftrightarrow t=-2\)
Do đó B(1;4) và đường thẳng \(\Delta\) cần tìm có phương trình x=1