Tìm b biết, a + b; b + c; c + a tỉ lệ nghịch với 3;8;12 và a + b + c = 26
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MM
0
15 tháng 7 2015
a) NHận thấy:
102:12=8 dư 6
Vậy q=8;r=6 để 102=12x8+6
b) Nhận thấy:
a=12x3+5
a=36+5
a=41
c) không biết làm
d) Ta có:
51-0=bxq
51=bxq
Mà 51=17x3
=1x51
Suy ra b=17 thì q=3
q=17 thì b=3
b=51 thì q=1
q=51 thì b=1
15 tháng 7 2015
a) Từ \(a=b.q+r\) nên \(q=a:b\) và r là số dư của phép chia này
q = 102 : 12 = 8 (dư r = 6)
b), c) d) tương tự thế mà làm nhé !
I
0
I
0
9 tháng 9 2023
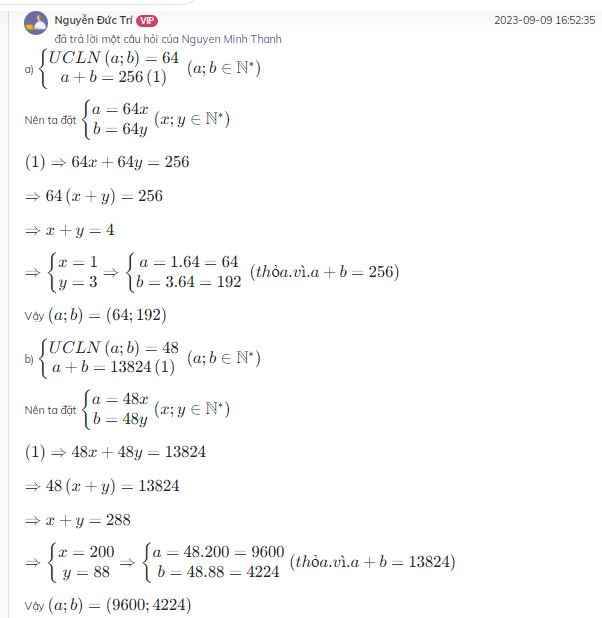
a) \(\left\{{}\begin{matrix}UCLN\left(a;b\right)=64\\a+b=256\left(1\right)\end{matrix}\right.\) \(\left(a;b\inℕ^∗\right)\)
Nên ta đặt \(\left\{{}\begin{matrix}a=64x\\b=64y\end{matrix}\right.\) \(\left(x;y\inℕ^∗\right)\)
\(\left(1\right)\Rightarrow64x+64y=256\)
\(\Rightarrow64\left(x+y\right)=256\)
\(\Rightarrow x+y=4\)
\(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1.64=64\\b=3.64=192\end{matrix}\right.\) \(\left(thỏa.vì.a+b=256\right)\)
Vậy \(\left(a;b\right)=\left(64;192\right)\)
b) \(\left\{{}\begin{matrix}UCLN\left(a;b\right)=48\\a+b=13824\left(1\right)\end{matrix}\right.\) \(\left(a;b\inℕ^∗\right)\)
Nên ta đặt \(\left\{{}\begin{matrix}a=48x\\b=48y\end{matrix}\right.\) \(\left(x;y\inℕ^∗\right)\)
\(\left(1\right)\Rightarrow48x+48y=13824\)
\(\Rightarrow48\left(x+y\right)=13824\)
\(\Rightarrow x+y=288\)
\(\Rightarrow\left\{{}\begin{matrix}x=200\\y=88\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=48.200=9600\\b=48.88=4224\end{matrix}\right.\) \(\left(thỏa.vì.a+b=13824\right)\)
Vậy \(\left(a;b\right)=\left(9600;4224\right)\)
TV
9 tháng 9 2023
b,Theo bài ra ta có:
a + b =13824
ƯCLN (a,b)=48
*Vì ƯCLN (a,b) =48 => a=48x (x < y, ƯCLN (x,y ) = 1)
b=48y
*Mà a + b = 13824
=> 48x + 48y = 13824
48(x + y) = 13824 : 48
x + y = 288
*Ta phải tìm hai số x,y thỏa mãn các điều kiện :
x < y
UCLN (x,y) = 1
x + y =4
=>Với x=1 thì y=3
Lập bảng:
x=1
y=3
a=288 . 1 = 288 thuộc N
b=288 . 3 = 864 thuộc N
Vậy a=288,b=864.
a,Theo bài ra ta có:
a + b =256
ƯCLN (a,b)=64
*Vì ƯCLN (a,b) =64 => a=64x (x < y, ƯCLN (x,y ) = 1)
b=64y
*Mà a + b = 256
=> 64x + 64y = 256
64(x + y) = 256 : 64
x + y = 4
*Ta phải tìm hai số x,y thỏa mãn các điều kiện :
x < y
UCLN (x,y) = 1
x + y =4
=>Với x=1 thì y=3
Lập bảng:
x=1
y=3
a=18 . 1 = 18 thuộc N
b=18 . 3 = 54 thuộc N
Vậy a=18,b=54.
TA
0
18 tháng 11 2021
- Ta có: a ≥ b ( a,b ∈ N )
ƯCLN ( a, b) = 16
⟹ a chia hết cho 16 ⟹ a = 16.m
⟹ b chia hết cho 16 ⟹ b = 16. n
(m, n là thương; m,n ∈ N, m ≥ n)
ƯCLN(m,n) = 1
⟹ a . b = ƯCLN.BCNN
mà a = 16. m
b = 16. n
Thay số: 16 . m . 16 . n = 16 . 240
16. m . 16. n = 3840
256. m. n = 3840
⟹ m. n = 3840 : 256 = 15
Ta có bảng sau :
| m | ... | ... | ... |
| n | ... | ... | ... |
| a | ... | ... | ... |
| b | ... | ... | ... |
⟹ Vậy (a,b) ∈ { (... , ...) ; (... , ....)}
AM
16 tháng 6 2015
a+b=-10
=>(a+b)2=100
=>a2+2ab+b2=100
=>a2+b2=100-2ab=100-2.24=52
=>a2+b2-2ab=52-2ab
=>(a-b)2=52-2.24=4
=>a-b=+-4
*)a-b=4
=>a=(4-10):2=-3
b=-7
*)a-b=-4
=>a=(-4-10):2=-7
b=-3
Ta có:140=22.5.7
Mà a-b=7
Thử các trường hợp ta không tìm thấy ab thõa mãn
SJ
16 tháng 6 2015
cho (a;b) là d => a = md ; b= nd
với m;n \(\in N^{\cdot}\) và (a;b) = 1
a -b \(\Leftrightarrow\) d(m-n) = 7 ; a > b => m > n [1]
từ \(ab=\left(a;b\right).\left[a;b\right]\Rightarrow\left[a;b\right]=\frac{ab}{\left(a;b\right)}\frac{mnd^2}{d}=dmn\) [2]
thừ [1] và [2] => d thuộng ƯC(7;140) mà ƯCLN( 7;140) = 7
=> d thuộc Ư(7)
thay d ta thấy chỉ có 7 là thik hợp
d = 7 thì m-n = 1 => m = 5; n = 4 ; a=35 ; d= 28
Ta có: a + b ; b +c ; c + a TLN với 3,8,12
=> (a + b).3 = (b + c). 8 = (c + a). 12
=> \(\frac{a+b}{\frac{1}{3}}=\frac{b+c}{\frac{1}{8}}=\frac{c+a}{\frac{1}{12}}\) và a+b+c = 26
Áp dụng tính chất dãy tỉ số bằng nhau
Ta có: \(\frac{a+b}{\frac{1}{3}}=\frac{b+c}{\frac{1}{8}}=\frac{c+a}{\frac{1}{12}}\)=\(\frac{a+b+b+c+c+a}{\frac{1}{3}+\frac{1}{8}+\frac{1}{12}}\)=\(\frac{2a+2b+2c}{\frac{13}{24}}\)=\(\frac{2.26}{\frac{13}{24}}=\frac{52}{\frac{13}{24}}=96\)
\(\frac{a+b}{\frac{1}{3}}=96\Rightarrow a+b=32\)
\(\frac{b+c}{\frac{1}{8}}=96\Rightarrow b+c=12\)
\(\frac{c+a}{\frac{1}{12}}=96\Rightarrow c+a=8\)
Ta có: a + b + c = 26
mà a + c = 8
=> b = 26 - 8 = 18
Vậy b = 18
@Nguyễn Huy Tú; @Trương Hồng Hạnh, @soyeon_Tiểubàng giải