Có bao nhiêu giá trị thực của tham số m thuộc (-10;10) để hàm số y=\(\sqrt{\left(m+1\right)x^2-2\left(m-1\right)x+3m-3}\) xác định với mọi x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 2 2019
Chọn B.
Phương pháp:
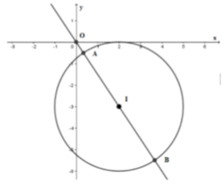
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
CM
9 tháng 9 2017
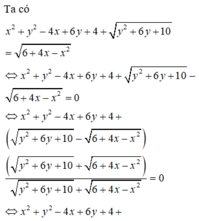
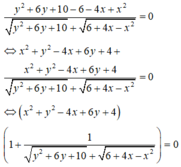
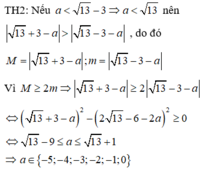
Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A
CM
5 tháng 8 2017
Đáp án C
Đặt m + e x = a ; e x = b a ≥ 0 ; b > 0 ta có:
m + b = a m + a = b ⇔ m + b = a 2 m + a = b 2
⇔ m + b = a 2 b − a = a 2 − b 2 ⇔ m + b = a 2 a − b a + b + 1 = 0 ⇒ m = a 2 − b a = b
( Do a ≥ 0 ; b > 0 )
Khi đó m = b 2 − b b > 0
Do b 2 − b ≥ − 1 4 ∀ b > 0 nên phương trình có nghiệm khi m ≥ − 1 4
Do đó có 10 giá trị nguyên của m ∈ − 1 4 ; 10 thỏa mãn yêu cầu bài toán.
CM
26 tháng 3 2018
Đáp án B.
Phương pháp:
Bất phương trình m ≥ f x , x ∈ D có nghiệm khi và chỉ khi m ≥ M i n D f x .
Cách giải:
ĐKXĐ: 0 < x < 1
3 log x ≤ 2 log m x − x 2 − 1 − x 1 − x ⇔ m x − x 2 − 1 − x 1 − x ≥ x x
⇔ m ≥ x x + 1 − x 1 − x x − x 2 , x ∈ 0 ; 1
Để bất phương trình đã cho có nghiệm thực thì m ≥ M i n 0 ; 1 f x , f x = x x + 1 − x 1 − x x − x 2
Xét
f x = x x + 1 − x 1 − x x − x 2 = x + 1 − x 1 − x x − 1 x x − 1 , x ∈ 0 ; 1
Đặt t = x + 1 − x , t ∈ 1 ; 2
Khi đó,
f x = x + 1 − x 1 − x 1 − x x 1 − x = t 1 − t 2 − 1 2 t 2 − 1 2 = t 3 − t 2 t 2 − 1 = 3 t − t 3 t 2 − 1 = g t
g ' t = − t 4 − 3 t 2 − 1 2 < 0 , ∀ t ∈ 1 ; 2
⇒ g t min = g 2 = 3 2 − 2 2 2 − 1 = 2 ⇒ M i n 0 ; 1 f x = 2 ⇒ m ≥ 2
Mà
m ∈ − 9 ; 9 ⇒ m ∈ 2 ; 3 ; 4 ; ... ; 8 ⇒
Có 7 giá trị thỏa mãn.
CM
10 tháng 6 2019
Chọn A.
Đặt 
. Với 
suy ra 1 ≤ t ≤ 2.
Phương trình đã cho trở thành t2 + t = 2m + 2 (*)
Phương trình đã cho có nghiệm thuộc đoạn 
có nghiệm 1 ≤ t ≤ 2
Xét hàm số f(t) = t2 + t với1 ≤ t ≤ 2 , ta thấy f’(t) = 2t + 1 nên f(t) là hàm đồng biến trên đoạn [1; 2]
Suy ra 2 = f(1) ≤ f(t) ≤ f(2) = 6
Vậy phương trình có nghiệm khi 2 ≤ 2m + 2 ≤ 6 hay 0 ≤ m ≤ 2
Suy ra có 3 giá trị nguyên m thỏa mãn yêu cầu bài toán.
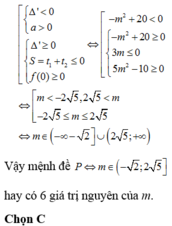
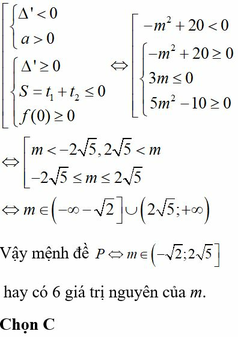
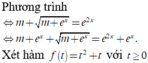
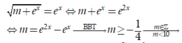
ycbt \(\Leftrightarrow\left(m+1\right)x^2-2\left(m-1\right)x+3m-3\ge0,\forall x\inℝ\)
\(\Leftrightarrow\left\{{}\begin{matrix}m+1>0\\\Delta'\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-1\\\left[-\left(m-1\right)\right]^2-\left(m+1\right)\left(3m-3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-1\\\left(m-1\right)^2-3\left(m-1\right)\left(m+1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-1\\\left(m-1\right)\left[m-1-3\left(m+1\right)\right]\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-1\\\left(m-1\right)\left(-2m-4\right)\le0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}m>-1\\\left[{}\begin{matrix}m\ge1\\m\le-2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow m\ge1\)
Vậy \(1\le m< 10\)
Sửa đề một chút là "Có bao nhiêu số nguyên..." chứ không phải "Có bao nhiêu số thực..." nhé, vì nếu là số thực thì sẽ có vô hạn số thỏa mãn rồi.
Khi đó \(m\in\left\{1;2;3;...;9\right\}\)
\(\Rightarrow\) Có 9 giá trị m thỏa ycbt.