Khoảng cách từ điểm \(A\left( {1;1} \right)\) đến đường thẳng \(\Delta :3x + 4y + 13 = 0\) bằng:
A. 1
B. 2
C. 3
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow AB \bot \left( {SA{\rm{D}}} \right)\\ \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\end{array}\)
b) Kẻ \(AH \bot SC \Rightarrow d\left( {A,SC} \right) = AH\)
Tam giác \(ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
Tam giác \(SAC\) vuông tại \(A\)\( \Rightarrow SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 3 \)
Tam giác \(SAC\) vuông tại \(A\) có đường cao \(AH\)\( \Rightarrow AH = \frac{{SA.AC}}{{SC}} = \frac{{a\sqrt 6 }}{3}\)
Vậy \(d\left( {A,SC} \right) = \frac{{a\sqrt 6 }}{3}\).

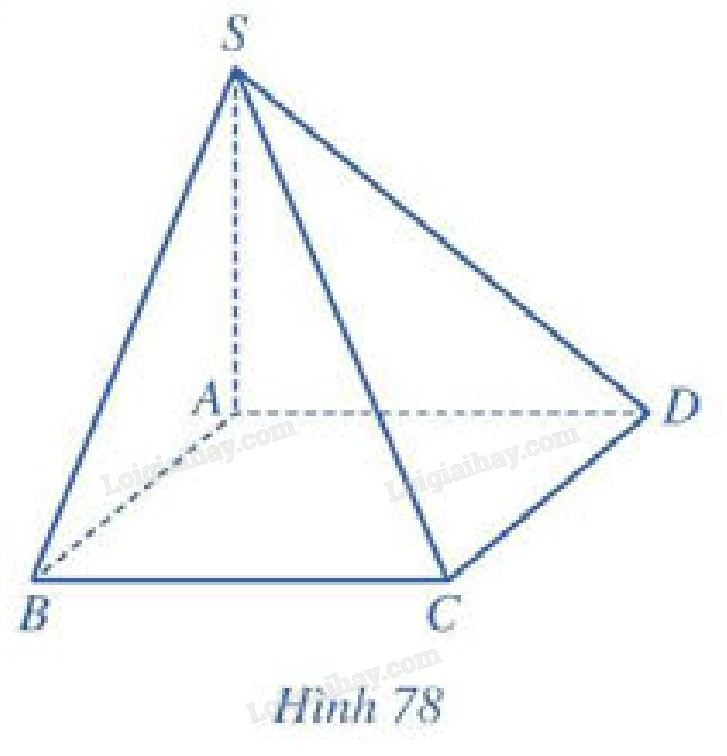
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).

a) Ta có: \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1 \Leftrightarrow x - 2y + 4 = 0\)
Vậy khoảng cách từ O đến \(\Delta \) là: \(d\left( {O;\Delta } \right) = \frac{{\left| {1.0 - 2.0 + 4} \right|}}{{\sqrt {{1^2} + {2^2}} }} = \frac{{4\sqrt 5 }}{5}\)
b) Lấy \(M\left( {0;1} \right) \in {\Delta _1}\)
Suy ra: \(d\left( {{\Delta _1},{\Delta _2}} \right) = d\left( {M,{\Delta _2}} \right) = \frac{{\left| {0 - 1 - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 \)

Trả lời:
Từ điền số 1 đến điểm 101 sẽ có: 101-1=100 khoảng bằng nhau.=> mỗi một khoảng bằng nhau có độ dài= 1m/100= 100cm/100=1cm
Từ điểm 13 đến điểm 31 có (31-13)=18 khoảng bằng nhau
=> Khoảng cách từ điểm 13 đến điểm 31 là: 18x1 cm= 18cm

Khoảng cách từ -1 đến 7 là
7 - ( -1) = 8
Khoảng cách từ -2 đến -8 là
-8 - -2 = -6
k nhé  Chu Quang Dũng
Chu Quang Dũng
Khoảng các từ -1 đến 7 lấy 7 - (-1 ) = 8
Khoảng cách từ -2 đến -8 là:
(-8) - (-2) = 6.
Đáp số: 8 ; 6.

Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$

Bài 1:
Nửa quãng đường AB( hay M cách A, B) dài là:
540:2=270(km)
Gọi quãng đường ô tô và xe máy đã đi lần lượt là S1; S2 (km) và t (giờ) là thời gian cần tìm.
Trong cùng 1 thời gian đi thì quãng đường tỉ lệ thuận với vận tốc.
\(\Rightarrow\frac{S_1}{65}=\frac{S_2}{40}=t\)
Ta có:
\(S_1=\frac{1}{2}\cdot S_2\)
\(\Rightarrow t=\frac{270-a}{65}=\frac{540-2a}{130}=\frac{270-2a}{40}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(t=\frac{540-2a}{130}=\frac{270-2a}{40}=\frac{\left(540-2a\right)-\left(270-2a\right)}{130-40}=\frac{270}{90}=3\)
Vậy sau khi khởi hành 3 giờ thì ô tô cách M 1 khoảng bằng \(\frac{1}{2}\) khoảng cách từ xe máy đến M.
Khoảng cách từ điểm \(A\left( {1;1} \right)\) đến đường thẳng \(\Delta :3x + 4y + 13 = 0\) bằng:
\(d\left( {A,\Delta } \right) = \dfrac{{\left| {3.1 + 4.1 + 13} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 4\)
Chọn D