Cho hàm số f(x) có đạo hàm liên tục trên \(\left[0;1\right]\) thỏa mãn: \(3f\left(x\right)+xf'\left(x\right)=x^{2018}\). Tính \(I=\int\limits^1_0f\left(x\right)dx\).
A. \(I=\frac{1}{2018.2021}\)
B. \(I=\frac{1}{2019.2020}\)
C. \(I=\frac{1}{2019.2021}\)
D....
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên \(\left[0;1\right]\) thỏa mãn: \(3f\left(x\right)+xf'\left(x\right)=x^{2018}\). Tính \(I=\int\limits^1_0f\left(x\right)dx\).
A. \(I=\frac{1}{2018.2021}\)
B. \(I=\frac{1}{2019.2020}\)
C. \(I=\frac{1}{2019.2021}\)
D. \(I=\frac{1}{2018.2019}\)
thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
. 
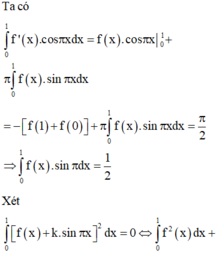
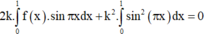
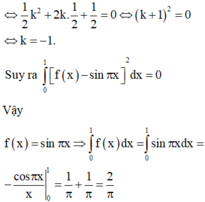
\(3f\left(x\right)+x.f'\left(x\right)=x^{2018}\Leftrightarrow3x^2.f\left(x\right)+x^3.f'\left(x\right)=x^{2020}\)
\(\Leftrightarrow\left(x^3.f\left(x\right)\right)'=x^{2020}\)
\(\Leftrightarrow x^3f\left(x\right)=\frac{1}{2021}x^{2021}+C\Rightarrow f\left(x\right)=\frac{x^{2018}}{2021}+\frac{C}{x^3}\)
Do \(f\left(x\right)\) có đạo hàm liên tục trên \(\left[0;1\right]\Rightarrow f\left(x\right)\) xác định tại \(x=0\Rightarrow C=0\)
\(\Rightarrow f\left(x\right)=\frac{x^{2018}}{2021}\)
Lấy tích phân 2 vế:
\(\int\limits^1_0f\left(x\right)dx=\int\limits^1_0\frac{x^{2018}}{2021}dx=\frac{1}{2019.2021}\)