Cho hàm số \(y=x^2-2x-1\). Mệnh đề nào sau đây sai? A.Hàm số giảm trên khoảng \(\left(-\infty

BL

Bùi Linh Nhi

17 tháng 10 2019

Cho hàm số \(y=x^2-2x-1\). Mệnh đề nào sau đây sai? A.Hàm số giảm trên khoảng \(\left(-\infty;1\right)\) B.Đồ thị hàm số có trục đối xứng x=-2 C.Đồ thị hàm số nhận I(1;-2) làm đỉnh D..Hàm số tăng trên khoảng \(\left(1;+\infty\right)\) Mọi người giải thích chi tiết cho em với ạ.Em cảm...

Đọc tiếp

#Toán lớp 10

1

NV

Nguyễn Việt Lâm

Giáo viên

17 tháng 10 2019

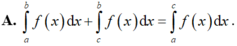
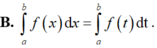
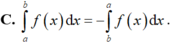
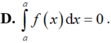
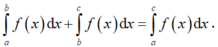
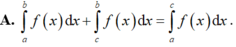
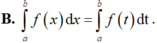
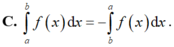
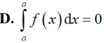
\(a=1>0;b=-2\Rightarrow\frac{-b}{2a}=1\)

Đồ thị hàm số có trục đối xứng \(x=1\)

Đúng(0)

PT

Phạm Trần Phát

7 tháng 8 2023

Câu 4. Cho hàm số \(y = x^4 - 2x^2 -3\). Mệnh đề nào sau đây là mệnh đề đúng?A. Hàm số nghịch biến trên \((-1; 0).\)B. Hàm số đồng biến trên \((-\infty;0).\)C. Hàm số nghịch biến trên \((-1; 1).\)D. Hàm số nghịch biến trên \((0;...

Đọc tiếp

#Toán lớp 12

3

GN

GV Nguyễn Trần Thành Đạt

Giáo viên

7 tháng 8 2023

\(y'=0\Leftrightarrow4x^3-4x=0\Leftrightarrow4x\left(x^2-1\right)=0\\ \Leftrightarrow x=\pm1.và.x=0\)

\(HSNB:\left(-\infty;-1\right)\cup\left(0;1\right)\\ HSĐB:\left(-1;0\right)\cup\left(1;+\infty\right)\)

Đúng(4)

TD

Tieen Ddat dax quay trow lai

7 tháng 8 2023

A

Đúng(0)

TC

Tâm Cao

18 tháng 5 2021

Trên khoảng nào sau đây, hàm số \(y=\sqrt{-x^2+2x}\) đồng biến ?

A. \(\left(1;+\infty\right)\)

B. (1;2)

C. (0;1)

D. \(\left(-\infty;1\right)\)

#Toán lớp 12

1

NV

Nguyễn Việt Lâm

Giáo viên

18 tháng 5 2021

ĐKXĐ: \(0\le x\le2\)

\(y'=\dfrac{-x+1}{\sqrt{-x^2+2x}}>0\Rightarrow x< 1\)

Kết hợp ĐKXĐ \(\Rightarrow\) hàm đồng biến trên \(\left(0;1\right)\)

Đúng(0)

PT

Pham Trong Bach

30 tháng 4 2019

Cho hàm số y=f(x) đồng biến trên khoảng (a;b). Mệnh đề nào sau đây sai?

A. Hàm số y=f(x+1) đồng biến trên khoảng (a;b)

B. Hàm số y=-f(x)+1 nghịch biến trên khoảng (a;b)

C. Hàm số y=f(x)+1 đồng biến trên khoảng (a;b)

D. Hàm số y=-f(x)-1 nghịch biến trên khoảng (a;b)

#Mẫu giáo

1

CM

Cao Minh Tâm

30 tháng 4 2019

Chọn A

Theo giả thiết ta có f’(x)≥0, (dấu bằng xảy ra tại hữu hạn điểm thuộc (a; b)).

Trên khoảng (a; b)

- Hàm số y = f(x)+1 có đạo hàm bằng f’(x) nên C đúng.

- Các hàm số y = - f(x)+1 và y = - f(x)-1 có đạo hàm bằng -f’(x) nên B, D đúng.

Do đó A sai

Đúng(0)

PT

Pham Trong Bach

15 tháng 2 2017

Cho hàm số y = f(x) đồng biến trên khoảng (a;b). Mệnh đề nào sau đây sai?

A. Hàm số y = f(x) +1 đồng biến trên khoảng (a;b)

B. Hàm số y = -f(x) + 1 nghịch biến trên khoảng (a;b).

C. Hàm số y = f(x) +1 đồng biến trên khoảng (a;b).

D. Hàm số y = -f(x) -1 nghịch biến trên khoảng (a;b)

#Toán lớp 12

1

CM

Cao Minh Tâm

15 tháng 2 2017

Chọn A

Theo giả thiết ta có (dấu bằng xảy ra tại hữu hạn điểm thuộc (a; b)).

Trên khoảng (a; b)

- Hàm số y = f(x) + 1 có đạo hàm bằng f’(x) nên C đúng.

- Các hàm số y = - f(x) + 1 và y = - f(x ) - 1 có đạo hàm bằng - f’(x) nên B, D đúng.

Do đó A sai

Đúng(0)

PT

Pham Trong Bach

6 tháng 1 2019

Cho hàm số y=f(x) đồng biến trên khoảng (a;b). Mệnh đề nào sau đây sai? A. Hàm số y=f(x+1) đồng biến trên (a;b) B. Hàm số y=f(x)+1 đồng biến trên (a;b) C. Hàm số y=-f(x) nghịch biến trên (a;b) D. Hàm số y=-f(x)-1 nghịch biến trên...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

6 tháng 1 2019

Ta có: Hàm số y=f(x) đồng biến trên khoảng a ; b ⇔ f ' ( x ) ≥ 0 , ∀ x ∈ a ; b , chỉ bằng 0 tại hữu hạn điểm trên (a;b).

+) Hàm số y=f(x)+1 có y ' = f ' ( x ) ≥ 0 , ∀ x ∈ ( a ; b ) , chỉ bằng 0 tại hữu hạn điểm trên (a;b).

⇒ y = f ( x ) + 1 đồng biến trên (a;b).

+) Hàm số y=-f(x) có y ' = - f ' ( x ) ≤ 0 , ∀ x ∈ ( a ; b ) , chỉ bằng 0 tại hữu hạn điểm trên (a;b).

⇒ y = - f ( x ) nghịch biến trên (a;b).

+) Hàm số y=-f(x)-1 có y ' = - f ' ( x ) ≤ 0 , ∀ x ∈ ( a ; b ) , chỉ bằng 0 tại hữu hạn điểm trên (a;b).

⇒ y = - f ( x ) - 1 nghịch biến trên (a;b).

+) Hàm số y=f(x+1) có y ' = f ' ( x + 1 ) : không có nhận xét về dấu dựa vào hàm số y=f(x)

Chọn đáp án A.

Đúng(0)

DM

Đoàn Minh Kiệt

13 tháng 6 2019 - olm

Cho hàm số y=-x²+5x+1

Giải thích vì sao có kết quả của các mệnh đề sau

A.Hàm số đồng biến trên khoảng(-∞;0)

B.Hàm số đồng biến trên khoảng(-∞;-1)

#Toán lớp 10

0

DM

Đoàn Minh Kiệt

13 tháng 6 2019 - olm

Cho hàm số y=-x²+5x+1

Giải thích vì sao có kết quả của các mệnh đề sau

A.Hàm số đồng biến trên khoảng(-∞;0)

B.Hàm số đồng biến trên khoảng(-∞;-1)

#Toán lớp 10

0

MR

Ma Ron

30 tháng 4 2023

cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)

#Toán lớp 10

1