Bài 1: Tìm (P): y = ax2 + bx + c biết (P) có đỉnh I(2;1) và đi qua điểm A(4,5). Lập bảng biến thiên và vẽ (P).
Bài 2: Tìm tham số m để phương trình: (m2 - 1)x + 2m = 5x - 2√6 nghiệm đúng ∀x ∈ R
Bài 3: Cho phương trình: (2m - 1)x2 - 2(2m - 3)x + 2m + 5 = 0 (1)
Tìm m để phương trình:
a) Có nghiệm.
b) Có hai nghiệm phân biệt x1, x2 sao cho x1 = -x2.
Bài 4: Giải các phương trình sau:
![]()
Bài 5: Giải hệ phương trình sau: ![]()
Bài 6: Cho ΔABC có A(-1;1); B(1;3); C(1;-1)
a. ΔABC là tam giác gì? Tính chu vi và diện tích.
b. Tìm tọa độ tâm I và tính bán kính đường tròn ngoại tiếp tam giác ABC
c. Tìm tọa độ điểm D có hoành độ âm sao cho ΔADC vuông cân tại D.


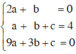
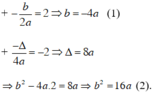
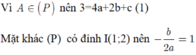
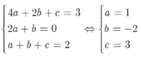
Đây mà lớp 1 á bạn???
tạo câu hỏi nhầm khối lớp rồi bạn=))