Cho G(2;1) tìm A thuộc d: 2x-y+1=0 ; d': x+y-1=0. Sao cho G là trọng tâm của tam giác ABO
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
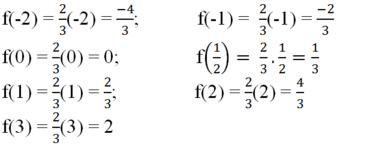
b) Ta có:
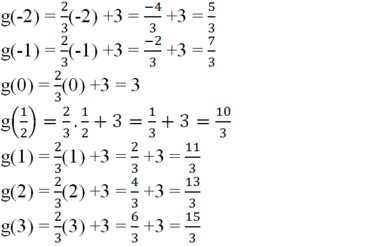
c) Từ kết quả câu a, b ta được bảng sau:

Nhận xét:
- Hai hàm số
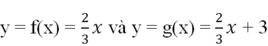
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.

Ta có: \(g\left(z\right)=3z-4\)
\(g\left(0\right)=3.0-4=-4\)
\(g\left(1\right)=3.1-4=-1\)
\(g\left(2\right)=3.2-4=2\)
\(g\left(-1\right)=3.\left(-1\right)-4=-7\)
\(g\left(-2\right)=3.\left(-2\right)-4=-10\)

a) f(-2) = -1; f(-1) = 0; f(0) = 1; f(2) = 3
g(-1) = 0,5; g(-2) = 2; g(0) = 0
b) f(x) = 2 ⇒ x = 1
g(x) = 2 ⇒ x = 2 hoặc x = -2

a) Thay f(-2) vào hàm số ta có :
y=f(-2)=(-2).(-2)+3=7
Thay f(-1) vào hàm số ta có :
y=f(-1)=(-2).(-1)+3=5
Thay f(0) vào hàm số ta có :
y=f(0)=(-2).0+3=1
Thay f(-1/2) vào hàm số ta có :
y=f(-1/2)=(-2).(-1/2)+3=4
Thay f(1/2) vào hàm số ta có :
y=f(1/2)=(-2).1/2+3=2
b) Thay g(-1) vào hàm số ta có :
y=g(-1)=(-1)2-1=0
Thay g(0) vào hàm số ta có :
y=g(0)=02-1=-1
Thay g(1) vào hàm số ta có :
y=g(1)=12-1=0
Thay g(2) vào hàm số ta có :
y=g(2)=22-1=3

c: Ở hai hàm số trên, nếu lấy biến x cùng một giá trị thì f(x) sẽ nhỏ hơn g(x) 3 đơn vị


Tìm hệ số a,b,c đấy à
Vì g ( x ) = ax2 + bx + c
=>\(\hept{\begin{cases}g\left(-2\right)=4a-2b+c=9\\g\left(-1\right)=a-b+c=2\\g\left(1\right)=a+b+c=6\end{cases}}\)
Giải hệ phương trình trên máy tính ta có :
a = 3
b = 2
c = 1
Study well
A thuộc d và B thuộc d'?
Do \(A\in d\Rightarrow A\left(a;2a+1\right)\)
\(B\in d'\Rightarrow B\left(b;1-b\right)\)
G là trọng tâm tam giác OAB
\(\Rightarrow\left\{{}\begin{matrix}x_A+x_B+x_O=3x_G\\y_A+y_B+y_O=3y_G\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=6\\2a+1+1-b=3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=6\\2a-b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\frac{7}{3}\\b=\frac{11}{3}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A\left(\frac{7}{3};\frac{17}{3}\right)\\B\left(\frac{11}{3};-\frac{8}{3}\right)\end{matrix}\right.\)