Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B là giao điểm của BD và AB nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+2y-7=0\\x+7y-7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=7\\y=0\end{matrix}\right.\) \(\Rightarrow B\left(7;0\right)\)
Đường chéo AC qua A và vuông góc BD nên nhận (2;-1) là 1 vtpt
Phương trình AC:
\(2\left(x-0\right)-1\left(y-1\right)=0\Leftrightarrow2x-y+1=0\)
Gọi I là giao điểm AC và BD \(\Rightarrow\) I là tâm hình thoi, tọa độ I thỏa mãn:
\(\left\{{}\begin{matrix}2x-y+1=0\\x+2y-7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow I\left(1;3\right)\)
I là trung điểm AC nên tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x_C=2x_I-x_A=2\\y_C=2y_I-y_A=5\end{matrix}\right.\) \(\Rightarrow C\left(2;5\right)\)
I là trung điểm BD nên tọa độ D thỏa mãn:
\(\left\{{}\begin{matrix}x_D=2x_I-x_B=-5\\y_D=2y_I-y_B=6\end{matrix}\right.\) \(\Rightarrow D\left(-5;6\right)\)

Đề bài hiển nhiên sai. Hình thoi này không thể tồn tại
Do hình thoi nên ABCD nên AB=BC \(\Rightarrow\Delta ABC\) cân tại B
\(\Rightarrow\widehat{BAC}=\widehat{BCA}\Rightarrow=120^0\)
Tam giác ABC có tổng 3 góc lớn hơn 180 độ (vô lý)

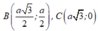
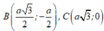
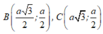
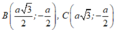
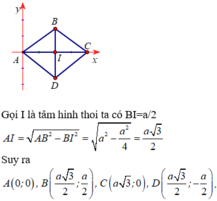





Giả sử hình thoi là ABCD với \(A\left(0;1\right)\)
Do tọa độ A thỏa \(x+7y-7=0\) nên đó là cạnh chứa A, ko mất tính tổng quát, giả sử đó là cạnh AB
Tọa độ A ko thỏa pt đường chéo nên đó là đường chéo BD
\(\Rightarrow\) Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+7y-7=0\\x+2y-7=0\end{matrix}\right.\) \(\Rightarrow B\left(7;0\right)\)
Phương trình AC qua A vuông góc BD: \(2\left(x-0\right)-1\left(y-1\right)=0\Leftrightarrow2x-y+1=0\)
Tọa độ tâm I là nghiệm: \(\left\{{}\begin{matrix}x+2y-7=0\\2x-y+1=0\end{matrix}\right.\) \(\Rightarrow I\left(1;3\right)\)
I là trung điểm AC \(\Rightarrow C\left(2;5\right)\)
I là trung điểm BD \(\Rightarrow D\left(-5;-3\right)\)
Biết tọa độ các đỉnh, bạn tự viết pt các cạnh nhé