Tìm tổng các giá trị của m để từ A (m;1) kẻ đúng 1 tiếp tuyến đến đồ thị hàm số y=\(\dfrac{2-x}{x-1}\) .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Phương trình x 2 − 2 x + m = 0
Có a = 1; b = -2; c = m nên b’= -1
⇒ Δ ' = ( − 1 ) 2 − 1 ⋅ m = 1 − m
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.
Khi đó, theo định lý Vi-et: 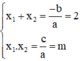
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.
b) Phương trình
x 2 + 2 ( m − 1 ) x + m 2 = 0 C ó ( a = 1 ; b = 2 ( m − 1 ) c = m 2 nên b ' = m − 1 ⇒ Δ ' = b ' 2 − a c = ( m − 1 ) 2 − m 2 = − 2 m + 1
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ - 2m + 1 ≥ 0 ⇔ m ≤ 1/2.
Khi đó, theo định lý Vi-et: 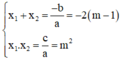
Vậy với m ≤ ½, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng m 2

Đáp án A
Điều kiện x ∈ ℝ
Đặt t = 2 sin x . Phương trình đã cho trở thành t 2 + 2 t = m ( * )
Vì sin x = sin α ⇔ x = α + 2 k π x = π − α + k 2 π nên để phương trình đã cho có tổng các nghiệm trong khoảng 0 ; π bằng π thì phương trình (*) phải có đúng một nghiệm t ∈ 1 ; 2 sin x ∈ 0 ; 1 thì 2 sin x ∈ 1 ; 2
Xét hàm số f t = t 2 + 2 t có bảng biến thiên
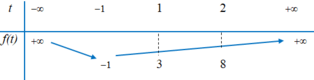
Suy ra để phương trình (*) có đúng một nghiệm t ∈ 1 ; 2 thì m ∈ 3 ; 8 .Vậy tổng các giá trị nguyên của m thỏa mãn yêu cầu bài toán là 4 + 5 + 6 + 7 = 22

Phương trình có 2 nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 13 4
⇔ a ≠ 0 Δ ≥ 0 − b a = 13 4 ⇔ m ≠ 0 m 2 − 3 3 − 4 m 2 ≥ 0 − m 2 − 3 m = 13 4
⇔ m ≠ 0 m 2 − 3 − 2 m m 2 − 3 + 2 m ≥ 0 4 m 2 + 13 m − 12 = 0
⇔ m ≠ 0 m + 1 m − 3 m − 1 m + 3 ≥ 0 m = 3 4 ; m = − 4
⇔ m ≠ 0 m ∈ − ∞ ; − 3 ∪ − 1 ; 1 ∪ 3 ; + ∞ m = 3 4 ; m = − 4 ⇔ m = 3 4 m = − 4
Vậy tổng bình phương các giá trị của m là: 265 16
Đáp án cần chọn là: A

\(M=\frac{6}{n-3}\)
a) Để M không là phân số
\(\Rightarrow n-3=0\)
\(\Rightarrow n=3\)
b) Để M là phân số và có giá trị nguyên
\(\Rightarrow n\ne3\)và \(6⋮n-3\)
\(6⋮n-3\)
\(n-3\in\left\{\pm6;\pm3;\pm2;\pm1\right\}\)
\(\Rightarrow n\in\left\{9;6;5;4;2;1;0;-3\right\}\)
a)Để \(M=\frac{-6}{n-3}\)không phải là p/s thì n-3 = 0 => n=3
Vậy nếu n=3 thì \(M=\frac{-6}{n-3}\)không phải là phân số.
b) Để \(M=\frac{-6}{n-3}\)là phân số thì \(n\ne3\), \(n\in Z\)và \(-6⋮n-3\)
\(-6⋮n-3\Leftrightarrow n-3\inƯ\left(-6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
Lập bảng
| n-3 | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| n | 4 | 3 | 5 | 1 | 6 | 0 | 9 | -3 |
Vậy nếu \(n\in\left\{0;1;\pm3;4;5;6;9\right\}\),\(n\in Z\)Và \(n\ne3\)thì \(M=\frac{-6}{n-3}\)là phân số và có gtrị nguyên

Phương trình x2 – 2x + m = 0
Có a = 1; b = -2; c = m nên b’= -1
⇒ Δ’ = (-1)2 – 1.m = 1 – m
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.
Khi đó, theo định lý Vi-et: 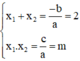
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.

Thay x = −3 vào phương trình
(m – 2)x2 – (m2 + 1)x + 3m = 0, ta có:
(m – 2) (−3)2 – (m2 + 1) (−3) + 3m = 0
⇔ 9m – 18 + 3m2 + 3 + 3m = 0
⇔ 3m2 + 12m – 15 = 0
⇔ m2 + 4m – 5 = 0
⇔ m2 – m + 5m – 5 = 0
⇔ m (m – 1) + 5 (m – 1) = 0
⇔ (m – 1) (m + 5) = 0 ⇔ m = 1 m = − 5
Suy ra tổng các giá trị của m là (−5) + 1 = −4
Đáp án cần chọn là: B

a) Để phương trình có 2 nghiệm phân biệt
<=> \(\Delta=\left[-\left(4m+3\right)^2\right]-4.2.\left(2m-1\right)=16m^2+24m+9-16m+8=16m^2+8m+1+16=\left(4m+1\right)^2+16>0\)
với mọi giá trị của m.
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m.
b) Vì phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m nên ta có: x1+x2= \(\dfrac{4m+3}{2}\)và x1.x2=\(\dfrac{2m-1}{2}\)



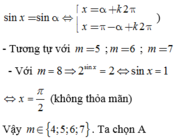
\(y'=\dfrac{-1}{\left(x-1\right)^2}\)
Gọi tiếp tuyến d qua A có dạng: \(y=k\left(x-m\right)+1\)
d là tiếp tuyến của (C) khi hệ sau có nghiệm: \(\left\{{}\begin{matrix}\dfrac{2-x}{x-1}=k\left(x-m\right)+1\\\dfrac{-1}{\left(x-1\right)^2}=k\end{matrix}\right.\)
\(\Rightarrow\dfrac{2-x}{x-1}=\dfrac{m-x}{\left(x-1\right)^2}+1\)
\(\Leftrightarrow-x^2+3x-2=m+x^2-3x+1\)
\(\Leftrightarrow-2x^2+6x-3=m\) (1)
Để từ A kẻ được đúng 1 tiếp tuyến \(\Rightarrow\) (1) có đúng 1 nghiệm thỏa mãn \(x\ne1\)
TH1: (1) có 1 nghiệm bằng 1 và 1 nghiệm khác 1 \(\Rightarrow m=1\)
TH2: đường thẳng \(y=m\) cắt \(y=-2x^2+6x-3\) tại đúng 1 điểm
\(\Rightarrow m=\dfrac{3}{2}\)