Question

[nguyễn hoàng lê thi]

4. Trong mặt phẳng toạ độ Oxy cho đg thẳng d có pt 2x -y +1=0. Để phép tịnh tiến theo vectơ v biến d thành chính nó thì vectơ v phải là vectơ nào ? Tại sao?

A. Vectơ v = (2;1)

B. Vectơ v = (2;-1)

C. Vectơ v= (1;2)

D. Vectơ v (-1;2)

15. Trong mặt phẳng với hệ trục toạ độ Oxy , cho các điểm A(-2;1) và B(2;-3). Phép tịnh tiến theo vectơ v biến điểm B thành điểm A . Hãy tìm toạ độ của vectơ u.

Answer 1

[Akai Haruma]

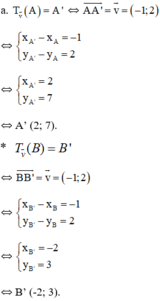
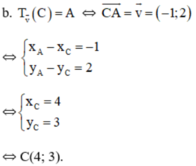
15.

Gọi $\overrightarrow{v}=(a,b)$

Theo bài ra ta có:

$T_{\overrightarrow{v}}(B)=A$

$\Leftrightarrow \overrightarrow{BA}=\overrightarrow{v}$

$\Leftrightarrow (-4,4)=\overrightarrow{v}$

Answer 2

[Akai Haruma]

4.

Bạn nhớ tính chất sau: phép tịnh tiến theo vecto $\overrightarrow{v}$ biến đường thẳng thành chính nó khi và chỉ khi $\overrightarrow{v}$ là vecto chỉ phương của đường thẳng $d$.

Dễ thấy $\overrightarrow{u_d}=(1,2)$ nên $\overrightarrow{v}=(1,2)$. Đáp án C.

Giải theo cách thuần thông thường:

Gọi vecto cần tìm là $\overrightarrow{v}=(a,b)$

Gọi $M(x,2x+1)$ là điểm thuộc đường thẳng $d$

$M'(x',y')=T_{\overrightarrow{v}}(M)\in (d)$

\(\Rightarrow \left\{\begin{matrix} x'=x+a; y'=2x+1+b\\ 2x'-y'+1=0\end{matrix}\right.\)

\(\Rightarrow 2(x+a)-(2x+1+b)+1=0\)

\(\Leftrightarrow 2a=b\)

Vậy $\overrightarrow{v}=(1,2)$