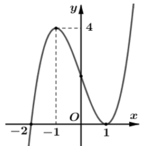
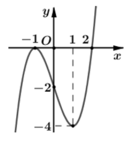
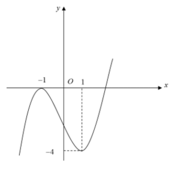
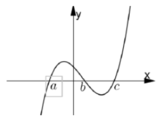
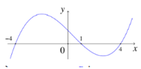
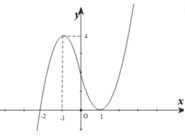
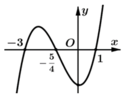
Cho hàm số y= f( x) = ax4+ bx3+ cx2+ dx+ e với a≠0. Đồ thị hàm số y= f’(x) như hình bên. Khẳng định nào sau đây sai?
A. Hàm số y= f(x) đồng biến trên ( -2; 1)
B. Hàm số y= f( x) đồng biến trên (1; + ∞)
C. Hàm số y= f(x) nghịch biến trên đoạn có độ dài nhỏ hơn 1000.
D. Hàm số y= f( x) nghịch biến trên (- ∞; -2)

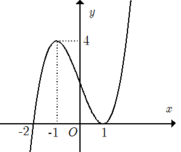
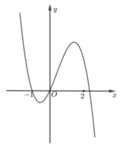
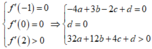

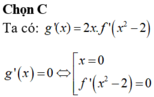
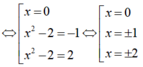
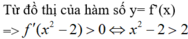
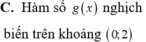
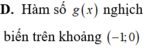


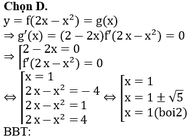

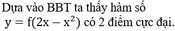



Chọn C
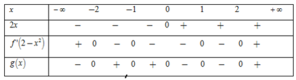
Dựa vào đồ thị của hàm số y= f’(x) ta thấy:
+ f’(x) > 0 khi x ∈ (-2;1) ∪ (1; + ∞)
=> Hàm số y= f(x) đồng biến trên các khoảng ( -2; 1) và ( 1; + ∞).
Suy ra A đúng, B đúng.
+ Ta thấy : f’(x)< 0 khi x< -2 ( chú ý nhận dạng đồ thị của hàm số bậc ba)
=> Hàm số y= f( x) nghịch biến trên khoảng ( - ∞; -2) .
Suy ra D đúng.
+ Dùng phương pháp loại trừ, ta chọn C