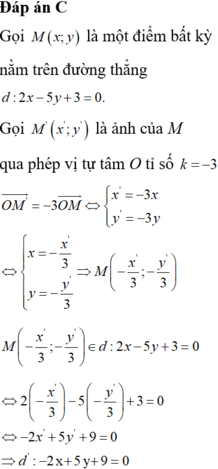Tìm ảnh của đường thẳng (A):2x−3y+6=0 qua phép vị tự tâm 7(2;1) có tỉ số vị tự k=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 5 2018
a) Lấy hai điểm A(0;4) và B(2;0) thuộc d. Gọi A′, B′ theo thứ tự là ảnh của A và B qua phép vị tự tâm O tỉ số k = 3. Khi đó ta có
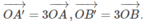
Vì O A → = ( 0 ; 4 ) nên O A ' → = ( 0 ; 12 ) . Do đó A′ = (0;12).
Tương tự B′ = (6;0); d1 chính là đường thẳng A'B' nên nó có phương trình:
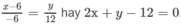
b) Có thể giải tương tự như câu a) .
Sau đây ta sẽ giải bằng cách khác.
Vì d 2 / / d nên phương trình của d 2 có dạng 2x + y + C = 0.
Gọi A′ = (x′;y′) là ảnh của A qua phép vị tự đó thì ta có:
I A ' → = − 2 I A → hay x′ + 1 = −2, y′ − 2 = −4
Suy ra x′ = −3, y′ = −2
Do A' thuộc d 2 nên 2.(−3) – 2 + C = 0.
Từ đó suy ra C = 8
Phương trình của d 2 là 2x + y + 8 = 0
CM
12 tháng 9 2019
Đáp án D
Phép vị tự biến đường thẳng thành đường thẳng song song với nó
Giả sử d ' : 2 x + y + m = 0 . Gọi A 0 ; 3 ⇒ T 0 ; k A ⇒ O A ' → = 2 O A → = 2 0 ; 3 ⇒ A ' 0 ; 6
Do đó 2.0 + 6 + m = 0 ⇒ m = − 6
