Cho hàm số y=sinx và \(\overrightarrow{v}=\left(\frac{-\pi}{2};0\right)\).Tìm ảnh của đồ thị hàm số y=sinx qua \(T\overrightarrow{v}\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Hàm số y = sinx đồng biến trên khoảng: \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
Chọn C
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
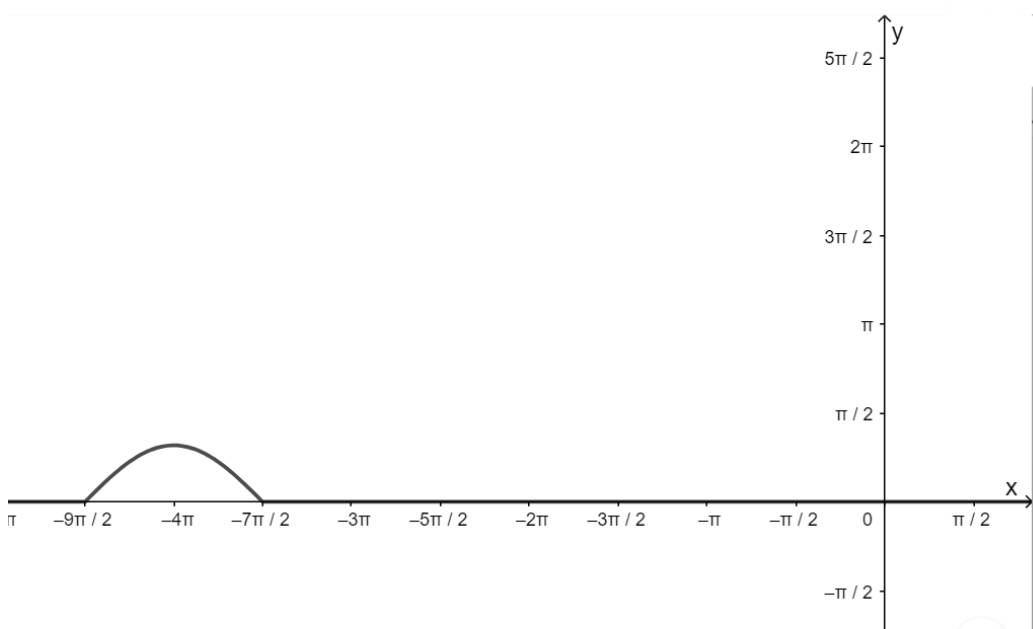
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
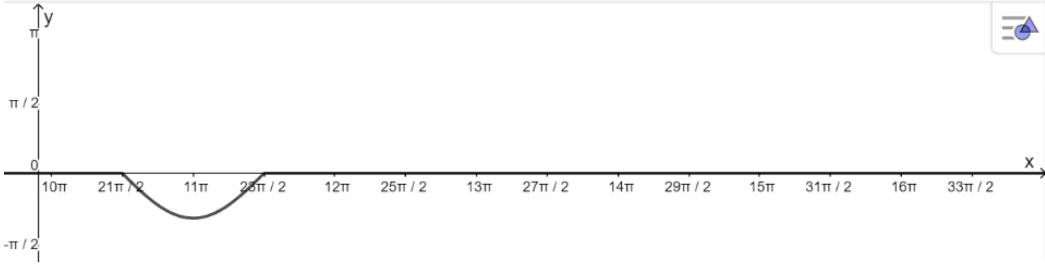
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Vẽ đồ thị:
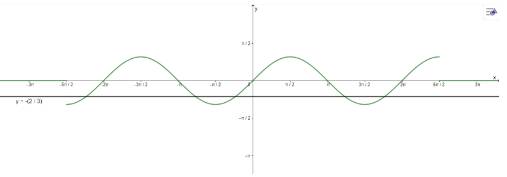
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:
\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Hàm số y = sinx nhận giá trị bằng 1
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = sinx và y = 1 là A, B,...
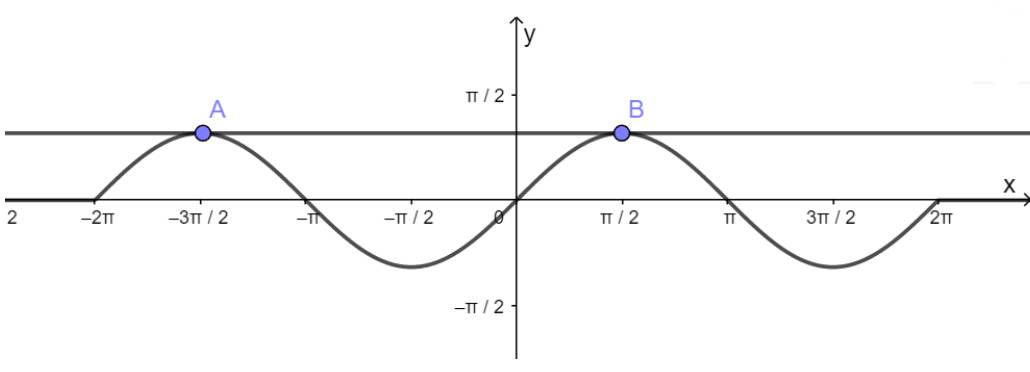
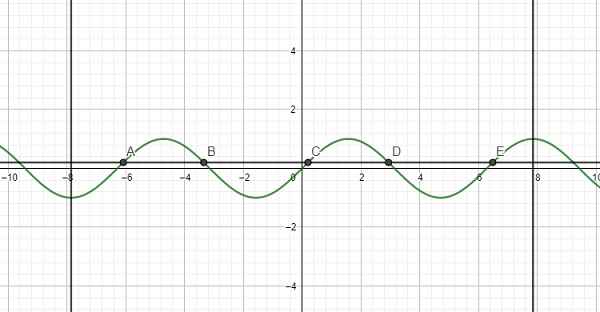
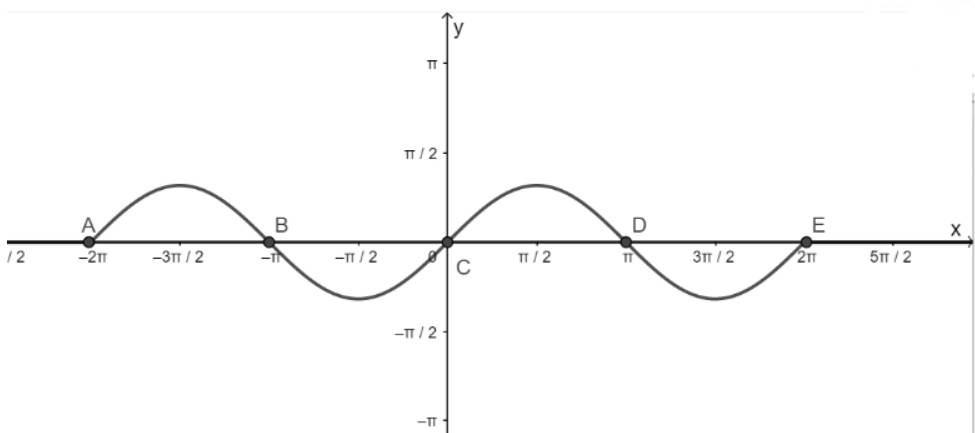
b) Hàm số y = sinx nhận giá trị bằng 0
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = sinx và y = 0 là A, B, C, D, E,...
c) Hàm số y = cosx nhận giá trị bằng – 1
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = cosx và y = - 1 là A, B,...
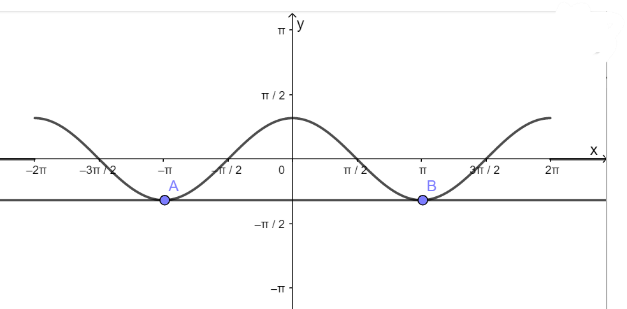
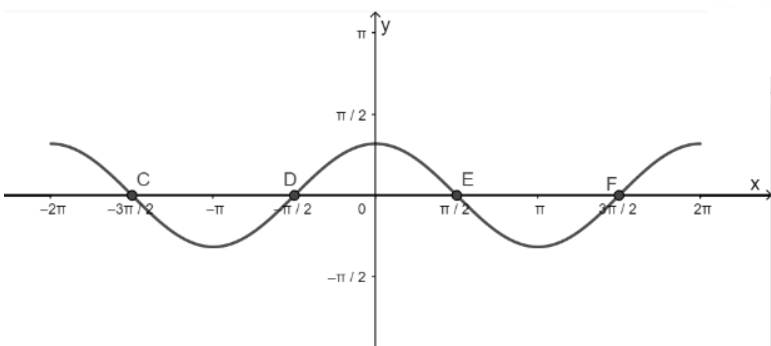
d) Hàm số y = cosx nhận giá trị bằng 0
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = cosx và y = 0 là C, D, E, F,...
HQ
Hà Quang Minh
Giáo viên
25 tháng 8 2023
Đồ thị của hàm số \(y=sin\left(x\right)\) trên đoạn \(\left[-\pi;\pi\right]\) là:
Ta thấy đồ thị hàm số giao với đường thẳng d: \(y=\dfrac{1}{2}\) tại 2 điểm.
Do đó, phương trình \(sin\left(x\right)=\dfrac{1}{2}\) có hai giá trị \(x\in\left[-\pi;\pi\right]\) thỏa mãn
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 9 2021
\(0< \dfrac{1}{2018}< 1\)
Kẻ 1 đường thẳng nằm ngang nằm giữa \(y=0\) và \(y=1\) ta thấy cắt đồ thị tại 5 điểm trên đoạn đã cho
\(\Rightarrow\) Pt có 5 nghiệm
