Cho hình chữ nhật ABCD có tâm \(I\left(\frac{1}{2};0\right)\) đường thẳng chứa cạnh AB có phương trình : \(x-2y+2=0\) và \(AB=2AD\).
Tìm tọa độ các đỉnh của hình chữ nhật, biết rằng đỉnh A có hoành độ âm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là tọa độ trung điểm của cạnh AD => M (1 ; 2)
Gọi N ( x N ; y N ) là tọa độ trung điểm của cạnh BC
Do I là tâm của hình chữ nhật nên I là trung điểm của MN.
Suy ra
x N = 2 x I − x M = − 3 y N = 2 y I − y M = − 2 ⇒ N − 3 ; − 2 .
Đáp án C

Gọi M là tọa độ trung điểm của cạnh AD => M (1 ; 2).
Gọi N ( x N ; y N ) là tọa độ trung điểm của cạnh BC.
Do I là tâm của hình chữ nhật nên I là trung điểm của MN.
Suy ra x N = 2 x I − x M = − 3 y N = 2 y I − y M = − 2 ⇒ N − 3 ; − 2 .
Đáp án C

I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:
\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)
Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
B là giao điểm AB và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)
I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)

Xét ΔABD vuông tại A có:
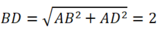
Do ABCD là hình chữ nhật tâm I nên:
AI = IC = ID = 1/2 BD = 1
ΔICD có ID = IC = DC = 1
⇒ΔICD đều ⇒ ∠(DIC) = 60o
Ta có: ∠(DIC) + ∠(AID ) = 180o⇒ ∠(AID ) = 180o- 60o= 120o
\(d\left(I;AB\right)=\frac{\left|\frac{1}{2}+2\right|}{\sqrt{1^2+\left(-2\right)^2}}=\frac{\sqrt{5}}{2}\Rightarrow AD=2d\left(I;AB\right)=\sqrt{5}\)và \(AB=2AD=2\sqrt{5}\)
Do đó \(IA=IB=IC=ID=\frac{1}{2}AC=\frac{5}{2}\)
Gọi \(\omega\) là đường tròn tâm I, bán kính \(R=IA\) thế thì \(\omega\) có phương trình \(\left(x-\frac{1}{2}\right)^2+y^2=\frac{25}{4}\)
Do vậy tọa độ của A, B là nghiệm của hệ :
\(\begin{cases}\left(x-\frac{1}{2}\right)^2+y^2=\frac{25}{4}\\x-2y+2=0\end{cases}\)
Giải hệ thu được \(A\left(-2;0\right);B\left(2;2\right)\) (do A có hoành độ âm), từ đó , do I là trung điểm của AC và BD suy ra \(C\left(3;0\right);D\left(-1;-2\right)\)