cho \(0\le a\le2;0\le b\le2;0\le c\le2\) và a+b+c=3. Chứng minh a^2+b^2+c^2\(\le\)5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 11 2018
\(-1\le a\le2\Rightarrow\hept{\begin{cases}a+1\ge0\\a-2\le0\end{cases}\Rightarrow\left(a+1\right)\left(a-2\right)\le0}\)
Tương tự \(\left(b+1\right)\left(b-2\right)\le0,\left(c+1\right)\left(c-2\right)\le0\)
=> (a+1)(a-2)+(b+1)(b-2)+(c+1)(c-2)\(\le\)0 => a2+b2+c2-(a+b+c)-6\(\le\)0
=>a2+b2+c2 \(\le\)6
Dấu "=" xảy ra <=> (a+1)( a-2)=0, (b+1)(b-2)=0, (c+1)(c-2)=0 , a+b+c=0 <=> a=2, b=c=-1 và các hoán vị
1N
cho ba số dương \(0\le a\le b\le c\le1\) CMR \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le2\)
1
25 tháng 5 2022
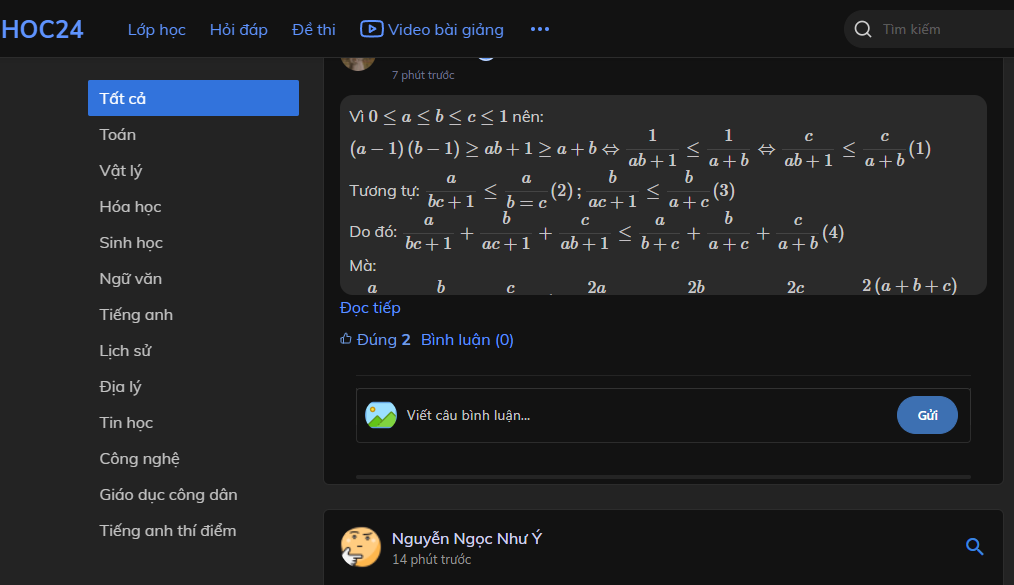
Vì \(0\le a\le b\le c\le1\) nên:
\(\left(a-1\right)\left(b-1\right)\ge ab+1\ge a+b\Leftrightarrow\dfrac{1}{ab+1}\le\dfrac{1}{a+b}\Leftrightarrow\dfrac{c}{ab+1}\le\dfrac{c}{a+b}\left(1\right)\)
Tương tự: \(\dfrac{a}{bc+1}\le\dfrac{a}{b=c}\left(2\right);\dfrac{b}{ac+1}\le\dfrac{b}{a+c}\left(3\right)\)
Do đó: \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\left(4\right)\)
Mà: \(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\le\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\left(5\right)\)
Từ (4) và (5) suy ra \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\left(đpcm\right)\)
DF
1
6 tháng 1 2021
Ta có \(\left(a+2\right)\left(b+2\right)\left(c+2\right)+\left(2-a\right)\left(2-b\right)\left(2-c\right)\ge0\)
\(\Leftrightarrow4\left(ab+bc+ca\right)+16\ge0\)
\(\Leftrightarrow ab+bc+ca\ge-4\).
Lại có: \(ab+bc+ca\le\dfrac{\left(a+b+c\right)^2}{3}=0\).
Do đó \(\left(ab+bc+ca\right)^2\le16\).
Mặt khác do \(a+b+c=0\) nên dễ dàng chứng minh được \(2\left(a^4+b^4+c^4\right)=\left(ab+bc+ca\right)^2\) (Bạn xem ở đây).
Do đó \(a^4+b^4+c^4\le32\) (đpcm).
DH
1
23 tháng 12 2017
Do \(a,b,c\in Z^+\)=> \(\frac{a}{a+b}>\frac{a}{a+b+c}\)\(\frac{b}{b+c}>\frac{b}{a+b+c}\)và \(\frac{c}{c+a}>\frac{c}{a+b+c}\)
\(\Rightarrow\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=1\)
Giả sử \(a\ge b\ge c\)Ta có \(a,b,c\in Z^+\)và \(a\ge b\)\(\Rightarrow\)\(c+a\ge c+b\)\(\Rightarrow\frac{c}{c+a}\le\frac{c}{c+b}\Rightarrow\frac{b}{b+c}+\frac{c}{c+a}\le\frac{b}{b+c}+\frac{c}{c+b}=1\)
Do \(a,b,c\in Z^+\)\(\Rightarrow\frac{a}{a+b}< 1\Rightarrow\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}< 2\)
Vậy \(\frac{a}{a+b}+\frac{c}{b+c}+\frac{a}{c+a}\le2\)
A
1
2 tháng 2 2018
Bài này lớp 7 là khó đấy \(0\le a\le b\le c\le1\Rightarrow\hept{\begin{cases}1-a\ge0\\1-b\ge0\end{cases}\Rightarrow\left(1-a\right)\left(1-b\right)\ge0}\)
\(\Leftrightarrow ab-a-b+1\ge0\Leftrightarrow ab+1\ge a+b\)(*)
Vì \(0\le a\le b\le c\le1\) nên \(\hept{\begin{cases}ab\ge0\\1\ge c\end{cases}\Rightarrow ab+1\ge c}\)Kết hợp với (*) ta được :
\(2\left(ab+1\right)\ge a+b+c\) \(\Leftrightarrow\frac{1}{ab+1}\le\frac{2}{a+b+c}\Rightarrow\frac{c}{ab+1}\le\frac{2}{a+b+c}\)(1)
Chứng minh tương tự \(\hept{\begin{cases}\frac{a}{bc+1}\le\frac{2a}{a+b+c}\text{ }\left(2\right)\\\frac{b}{ac+1}\le\frac{2b}{a+b+c}\text{ }\left(3\right)\end{cases}}\)
Cộng vế với vế của (1);(2);(3) ta được :
\(\frac{a}{bc+1}+\frac{b}{ac+1}+\frac{c}{ab+1}\le\frac{2\left(a+b+c\right)}{a+b+c}=2\)(đpcm)
Vì \(0\le a\le2;0\le b\le2;0\le c\le2\Rightarrow\left(2-a\right)\left(2-b\right)\left(2-c\right)\ge0\)\(\Leftrightarrow8-4\left(a+b+c\right)+2\left(ab+bc+ca\right)-abc\ge0\)\(\Leftrightarrow2\left(ab+bc+ca\right)\ge4\left(a+b+c\right)-8+abc\ge4\)\(\Leftrightarrow2\left(ab+bc+ca\right)\ge12-8+abc\ge4\)
\(\Rightarrow\)\(2\left(ab+bc+ca\right)\ge4\)
\(\Leftrightarrow-2\left(ab+bc+ca\right)\le-4\)
Ta có :
\(a+b+c=3\Rightarrow\left(a+b+c\right)^2=9\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=9\)
\(\Rightarrow a^2+b^2+c^2=9-2\left(ab+bc+ca\right)\le9-4=5\Rightarrowđpcm\)Đẳng thức xảy ra khi
\(\left(2-a\right)\left(2-b\right)\left(2-c\right)=0\)
\(\left[{}\begin{matrix}2-a=0\\2-b=0\\2-c=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}a=2\\b=2\\c=2\end{matrix}\right.\)