Cho parabol (P): y=ax2+bx+c Tìm các giá trị nguyên m\(\in\)[-9;0) để phương trình -x2-4x=m+3 có 2 nghiệm phân biệt nhỏ hơn hoặc bằng 1.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
D
1

NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2021
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\\dfrac{4ac-b^2}{4a}=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-4a\\12a-16a^2=-8a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=-4a\\a=\dfrac{5}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{4}\\b=-5\end{matrix}\right.\)
\(\Rightarrow a+2b=...\)
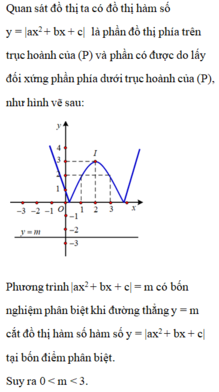
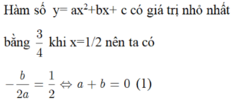
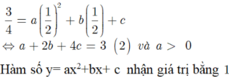
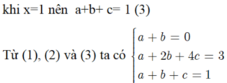
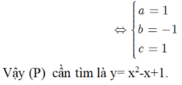







ta có phương trình tương đương
\(x^2+4x+4=1-m\Leftrightarrow\left(x+2\right)^2=1-m\) có hai nghiệm phân biệt khi \(1-m>0\Leftrightarrow m< 1\)
Khi đó hai nghiệm sẽ là : \(\hept{\begin{cases}x=-2+\sqrt{1-m}\\x=-2-\sqrt{1-m}\end{cases}}\) hai nghiệm nhỏ hơn hoặc bằng 1 nên ta có :
\(-2-\sqrt{1-m}< -2+\sqrt{1-m}\le1\)\(\Leftrightarrow\sqrt{1-m}\le3\Leftrightarrow-8\le m\)
mà \(m\in\text{[-9,0)}\Rightarrow\text{ có 8 giá trị nguyên của m thỏa mãn đề bài}\)
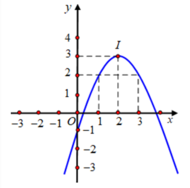
số nghiệm của phtrinh -x2 - 4x = m + 3 chính là số giao điểm của parabol y = -x2 - 4x và đường thẳng y = m + 3
ở đây mình sẽ dùng phương pháp quan sát đồ thị nhé:D
nhìn vào đồ thị, để phtrinh -x2 - 4x = m + 3 có 2 nghiệm phân biệt nhỏ hơn hoặc bằng 1 thì parabol phải cắt đường thẳng tại 2 điểm phân biệt có hoành độ nhỏ hơn hoặc bằng 1 => \(4>m+3\ge-5\Leftrightarrow1>m\ge-8\)
lại có: m\(\in\)[-9; 0) => m \(\in\)[-8; 0] và m nguyên => m \(\in\)\(\left\{-8;-7;-6;...;-1\right\}\)