Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;4;5), B(3;4;0), C(2;-1;0) và mặt phẳng ( P ) : 3 x - 3 y - 3 z - 12 = 0 . Gọi M(a;b;c) thuộc (P) sao cho M A 2 + M B 2 + 3 M C 3 đạt giá trị nhỏ nhất. Tính tổng a+b+c.
A. 3.
B. 2
C. –2.
D. –3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
A B → = 0 ; 4 ; 2 , A C → = − 3 ; 4 ; 3
A B C qua A 3 ; − 2 ; − 2 và có véc tơ pháp tuyến A B → , A C → = 4 ; − 6 ; 12 = 2 2 ; − 3 ; 6
⇒ A B C : 2 x − 3 y + 6 z = 0

Đáp án C.
Ta có:
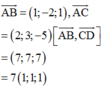
Vậy mặt phẳng (ABC) đi qua điểm A(1;1;1) và có một VTPT là n → ( 1 ; 1 ; 1 ) có phương trình
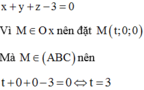
Đáp án A