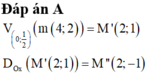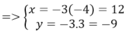Trong mặt phẳng tọa độ Oxy, phép đống dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k=1/2 và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ:
A. (2;-1)
B. (8;1)
C. (4;-2)
D. (8;4)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
9 tháng 3 2019
Đúng(0)
Những câu hỏi liên quan
CM
25 tháng 11 2018
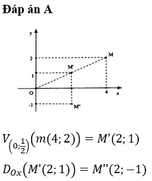
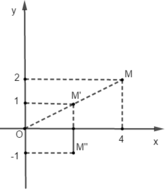
V ( 0 ; 1 / 2 ) ( M ( 4 ; 2 ) ) = M ' ( 2 ; 1 ) ; Đ O x ( M ' ( 2 ; 1 ) ) = M " ( 2 ; - 1 ) .
Đáp án A.
CM
9 tháng 1 2017
Phương trình đường thẳng d: x - y - 1= 0
Lấy M(x; y) thuộc d
Phép vị tự tâm O(0; 0) tỉ số k = 3 biến điểm M thành M’(x’; y’) thì O M ' → = 3 O M → ⇔ x ' = 3 x y ' = 3 y ⇔ x = 1 3 x ' y = 1 3 y '
Phép đối xứng trục Ox biến M’(x’; y’) thành M’’(x’’; y’’)
Thay vào phương trình d ta được: ⇔ x ' ' = x ' y ' ' = − y ' ⇔ x = 1 3 x ' ' y = − 1 3 y ' '
Hay x’’ + y’’ - 3 = 0
Vậy phương trình đường thẳng d’: x + y - 3 = 0.
Đáp án B
CM
21 tháng 3 2018
Phép vị tự tâm O(0; 0) tỉ số k = -5, biến M(x; y) thuộc d thành M’(x’, y’) thuộc d’ ⇒ O M ' → = - 5 O M →
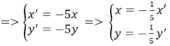
Thay vào phương trình d ta được:
2 . − 1 5 x ' + 3. − 1 5 y ' − 4 = 0 ⇔ − 2 5 x ' + − 3 5 y ' − 4 = 0 ⇔ 2 x ' + 3 y ' + 20 = 0
⇒ phương trình của d’ là 2x + 3y + 20 = 0
Đáp án D
CM
30 tháng 4 2017
Đáp án B
d cắt Ox,Oy lần lượt tại A − 3 ; 0 ; B 0 ; − 3 2 Qua phép quay tâm O góc quay − 90 ° điểm A và B lần lượt biến thành các điểm A ' 0 ; 3 ; B − 3 2 ; 0 ⇒ A ' B ' : 2 x − y + 3 = 0
Phép vị tự biến đường thẳng thành đường thẳng song song với nó nên d ' : 2 x − y + m = 0
Qua V O ; k A ' = A 1 ⇒ O A 1 → = 5 O A ' → ⇒ A 1 0 ; 15 ⇒ d ' : 2 x − y + 15 = 0
CM
23 tháng 5 2017
Phép vị tự tâm I(1; 2) tỉ số k = 5 biến điểm M(2; -3) thành điểm M’(x; y)
⇔ I M ' → = 5 I M → ⇔ x − 1 = 5 2 − 1 y − 2 = 5 − 3 − 2 ⇔ x = 6 y = − 23
Suy ra M’(6; -23).
Đáp án C