Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B.
Phương pháp: Tìm điều kiện để phương trình hoành độ giao điểm có ba nghiệm phân biệt thỏa mãn x A = 2 , hoặc x B < - 1 < x C < 1 hoặc - 1 < x B < 1 < x C
Cách giải:
Đồ thị hàm số y = x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 luôn đi qua điểm A(2;0)
Xét phương trình hoành độ giao điểm
x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 = 0
![]()
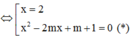
Để phương trình có 3 nghiệm phân biệt ó pt (*) có 2 nghiệm phân biệt khác 2
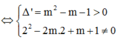
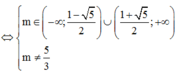
Giả sử x B ; x C ( x B < x C ) là 2 nghiệm phân biệt của phương trình (*).
Để hai điểm B, C một điểm nằm trong một điểm nằm ngoài đường tròn x2 + y2 = 1
TH1: ![]()
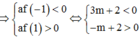
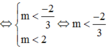
TH2: ![]()
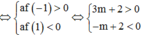
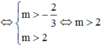
Kết hợp điều kiện ta có: 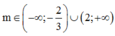
Lại có m ∈ [–10;100]
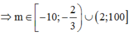
=> Có 108 giá trị m nguyên thỏa mãn yêu cầu bái toán

Đường tròn (S) tâm \(I\left(-1;-3\right)\) bán kính \(R=3\)
Thế tọa độ A vào pt (S) thỏa mãn nên A nằm trên đường tròn
Ta cần tìm B, C sao cho chi vi ABC lớn nhất
Đặt \(\left(AB;AC;BC\right)=\left(c;b;a\right)\Rightarrow\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}=2R\)
\(\Rightarrow a+b+c=2R\left(sinA+sinB+sinC\right)\)
Mặt khác ta có BĐT quen thuộc \(sinA+sinB+sinC\le\dfrac{3\sqrt{3}}{2}\)
Dấu "=" xảy ra khi tam giác ABC đều
\(\Rightarrow a=b=c=2R.sin60^0=3\sqrt{3}\)
Khi đó I đồng thời là trọng tâm kiêm trực tâm \(\Rightarrow\left\{{}\begin{matrix}BC\perp AI\\d\left(A;BC\right)=\dfrac{a\sqrt{3}}{2}=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow\) Phương trình BC có dạng \(y=-\dfrac{3}{2}\)
Hay (Cm) có 1 tiếp tuyến là \(y=-\dfrac{3}{2}\) (hệ số góc bằng 0 nên tiếp tuyến này đi qua 2 cực tiểu)
\(\Rightarrow m=-1\)

(C) giao Ox tại 3 điểm <=> x^3-(2m+1)x^2-9x=0 có 3nghiệm pbiệt
<=> x( x^2- ( 2m+1)x-9)=0 có 3 nghiệm pbiệt
<=> x=0
x^2- ( 2m+1)x-9=0 (*)có 2 nghiệm pbiệt <=> denta >0
gọi x1, x2 là 2 nghiệm của (*)
3 nghiệm của đề là x1;0 ; x2
ta có x1+x2=0 dùng viet
phuong trinh hoanh do giao diem la: x3-(2m+1)x2-9x=0. <=> x[x2 -(2m+1)x-9] =0 ta giai dc x=o va x2-(2m+1)x-9=0 ta dat g(x)=x2-(2m+1)x-9 de cm cat truc hoanh tai 3 diem pb thi g(x)=o phai co 2 nghiem pb khac 0. <=>Δ>0 =>m goi x1, x2 la nghiem cua g(x) de lap thanh cap so cong thi x2=9x1 Ap dung vi-et tim ra la dc![]()

Đáp án B
y = 0 ⇔ x 2 = 1 x 2 = 2 m + 1 . có 4 nghiệm phân biệt khi
2 m + 1 > 0 ; 2 m + 1 ≠ 1 ⇔ m > − 1 ; m ≠ 0 .
Khi đó 4 nghiệm là − 2 m + 1 ; − 1 ; 1 ; 2 m + 1
4 nghiệm lập thành cấp số cộng có trường hợp sau sắp xếp theo thứ tự sau
TH1: − 1 ; − 2 m + 1 ; 2 m + 1 ; 1 ⇒ khoảng cách giữa chúng là bằng nhau ⇔ 1 − 2 m + 1 = 2 2 m + 1 ⇔ 3 2 m + 1 = 1 ⇔ m = − 4 9 .
TH2: − 2 m + 1 ; − 1 ; 1 ; 2 m + 1 ⇒ khoảng cách giữa chung là bằng nhau
⇔ 2 m + 1 − 1 = 2 ⇔ m = 4
Lời giải:
PT hoành độ giao điểm:
\(x^3-2(m+1)x^2+(5m+1)x-2m-2=0\)
\(\Leftrightarrow (x-2)(x^2-2mx+m+1)=0\)
Vì \(A(2,0)\) nên hoành độ hai điểm \(B,C\) sẽ là nghiệm của PT \(x^2-2mx+m+1=0\)
Điều kiện: \(\Delta'=m^2-(m+1)>0\)
Khi đó, áp dụng định lý Viete, nếu $x_1,x_2$ là hai nghiệm của PT thì \(\left\{\begin{matrix} x_1+x_2=2m\\ x_1x_2=m+1\end{matrix}\right.\)
Nhận thấy hai điểm $B,C$ nằm trên $Ox$ mà một điểm nằm trong đường tròn \(x^2+y^2=1\) nên \((x_1-1)(x_2-1)<0\)
\(\Leftrightarrow x_1x_2-(x_1+x_2)+1<0\Leftrightarrow m+1-2m+1<0\)
\(\Leftrightarrow m>2\). Thử lại ta thấy thỏa mãn điều kiện \(\Delta'\)
Vậy \(m>2\)