Cho đường thẳng (d): y= (m - 2)x+n (m \(\ne\) 2)
Tìm giá của m và n trong mỗi trường hợp sau:
a) (d) đi qua 2 điểm A(-1;2) và B(3;-4)
b) (d) cắt trực tung tại điểm có tung độ \(=1-\sqrt{2}\) và cắt trục hoành tại điểm có hoành độ \(=2+\sqrt{2}\)
c) (d) cắt đường thẳng \(y=-\frac{3}{2}x+\frac{1}{2}\)
d) (d) trùng với đường thẳng y= 2x-3

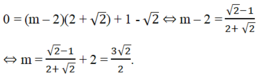
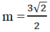 thì đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1 -
2
và cắt trục hoành tại điểm có hoành độ 2 +
thì đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1 -
2
và cắt trục hoành tại điểm có hoành độ 2 +
a) lần lượt cho x=-1, y=2 vào đường thẳng y=(m-2)x+n
ta có 2=-(m-2)+n
tương tự như vậy cho x=3, y=-4 ta có đường thẳng -4=(m-2)*3+n
sau đó cho 2 đường thẳng tương đương
suy ra m=0,5=1/2;
suy ra n=0,5=1/2
vậy m=0,5, n=0,5 thì (d) đi qua 2 điểm A(-1;2) và B(3;-4)
d) vì hai đương thẳng trùng nhau nên có a=a' , b=b'
mà a=m-2, b=n
a'=2 , b'=-3
suy ra m=4, n=-3
vậy m=4, n=-3 thì hai đường thẳng trùng nhau
c) vì hai đương thẳng cắt nhau có a#a', b=b'
mà a=m-2, b=n
a'=-1,5, b'=0,5
nên m-2 # -1,5
n=0,5
suy ra m # 0,5
n=0,5
vậy m # 0,5, n=0,5 thì hai đương thẳng cắt nhau