Cho hàm số y = f x có bảng biến thiên như dưới đây:
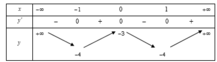
Tọa độ điểm cực đại của đồ thị hàm số y = f x là:
A. (1;-4)
B. (-1;-4)
C. x = 0
D. (0;-3)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
(I) sai f xđ trên R
(II) sai hs có 2 điểm cực trị
(III) ,(IV) đúng

Đáp án C
Từ bảng biến thiên ta thấy f x ≥ 1 > 0 , ∀ x > − 1 nên phương trình f(x) = 0 có một nghiệm duy nhất x 0 < − 1
Mặt khác ta có y = f x = f x , f x ≥ 0 f x , f x < 0
Do đó ta có bảng biến thiên của y= f x
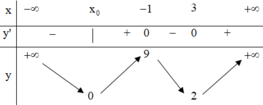
Từ bảng biến thiên ta thấy đồ thị hàm số y= f x có 3 điểm cực trị

Đáp án D
Ta vẽ lại bảng biến thiên của f x .

Từ bảng biến thiên này hàm số y = f x có cực trị

Chọn B.
Số điểm cực trị của đồ thị hàm số y=|f(x)| bằng số điểm cực trị của đồ thị hàm số y=f(x) cộng với số giao điểm của đồ thị hàm số y=f(x) với trục hoành (không tính điểm cực trị)
Vì đồ thị hàm số y=f(x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm trên đồ thị hàm số y=|f(x)| có 2 + 1 = 3 điểm cực trị

Chọn B.
Cách 1: Số điểm cực trị của đồ thị hàm số y=|f(x)| bằng số điểm cực trị của đồ thị hàm số y=f(x) cộng với số giao điểm của đồ thị hàm số y=f(x)với trục hoành (không tính điểm cực trị)
Vì đồ thị hàm số y=f(x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm nên đồ thị hàm số y=|f(x)| có 2 + 1 = 3 điểm cực trị

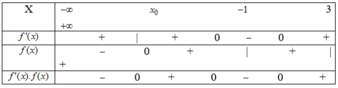
Đáp án: 3 cực trị

Kẻ đường thẳng y=0 đồ thị x=a>2 tại điểm duy nhất có hoành độ
Chọn đáp án A.
Chọn đáp án D.
Quan sát bảng biến thiên ta thấy hàm số có giá trị cực đại bằng -3 khi x = 0.Vậy tọa độ điểm cực đại của đồ thị hàm số là (0;-3)