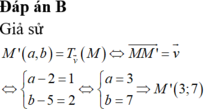Trong mp Oxy, cho M(-1;1), N(1;-3). Viết phương trình đường tròn đi qua 2 điểm M,N và có tâm nằm trên đường thẳng d: \(2x-y+1=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
I là trung điểmđoạn MM’ Áp dụng công thức tọa độ trung điểm để tính

Câu 1:
Theo đề, ta có: \(\overrightarrow{IM'}=-2\cdot\overrightarrow{IM}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=-2\cdot\left(-7-2\right)=18\\y-3=-2\cdot\left(2-3\right)=2\end{matrix}\right.\Leftrightarrow M'\left(20;5\right)\)

Câu 1:
Gọi G là trọng tâm tam giác \(\Rightarrow G\left(1;1\right)\)
\(\overrightarrow{BC}=\left(1;4\right)\Rightarrow\) đường thẳng d nhận \(\left(1;4\right)\) là 1 vtpt
Phương trình d:
\(1\left(x-1\right)+4\left(y-1\right)=0\Leftrightarrow x+4y-5=0\)
Câu 2:
Có 2 trường hợp thỏa mãn:
- Đường thẳng đi qua M và trung điểm AB
- Đường thẳng qua M và song song AB
TH1:
Gọi N là trung điểm AB \(\Rightarrow N\left(-1;2\right)\Rightarrow\overrightarrow{MN}=\left(-11;0\right)\)
\(\Rightarrow\) Đường thẳng MN nhận \(\left(0;1\right)\) là 1 vtpt
Phương trình MN:
\(0\left(x-10\right)+1\left(y-2\right)=0\Leftrightarrow y-2=0\)
TH2: \(\overrightarrow{AB}=\left(-8;4\right)=-4\left(2;-1\right)\)
Đường thẳng d song song AB nên nhận \(\left(1;2\right)\) là 1 vtpt
Phương trình d:
\(1\left(x-10\right)+2\left(y-2\right)=0\Leftrightarrow x+2y-14=0\)

Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)

Đường thẳng đi qua hai điểm A và B nhận \(\overrightarrow{AB}=\left(-2;-4\right)\) làm vecto chỉ phương.
Phương trình đường thẳng AB là \(\dfrac{x-1}{-2}=\dfrac{y-3}{-4}\Leftrightarrow2x-y+1=0\)
\(P=MA+MB\) đạt giá trị nhỏ nhất khi M, A, B thẳng hàng
\(\Leftrightarrow M\) là giao điểm của đường thẳng AB và d
\(\Leftrightarrow M\) có tọa độ nghiệm của hệ \(\left\{{}\begin{matrix}x-2y+3=0\\2x-y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow M\left(\dfrac{1}{3};\dfrac{5}{3}\right)\)

Đáp án A
Phép tịnh tiến biến(d) thành chính nó là phép tịnh tiến theo vectơ chỉ phương v → của (d) : v → ( 2019 ; − 2018 ) = k u → = 0 ; k m =>m = 0
=>có một giá trị m = 0 để biến (d) thành chính nó

Đáp án A
Phép tịnh tiến biến (d) thành chính nó là phép tịnh tiến theo vectơ chỉ phương của (d)
v → ( 2019 ; − 2018 ) = k u → = 2019 k ; k m => k = 1 m = – 2018
=>có một giá trị m = – 2018 để biến (d) thành chính nó

gọi M có tọa độ là (x;y) do M thuộc Ox=> tọa ddoooj M là (x;0)
ta có : \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\left(-2-X;5\right)+\left(3-X;-1\right)+\left(7-X;1\right)\right|\)
=\(\left|\sqrt{\left(-2-X\right)^2+5^2}+\sqrt{\left(3-X\right)^2+1}+\sqrt{\left(7-X\right)^2+1}\right|\)
=> BẠN TÌ gtnn CÁI TRONG LÀ ĐC