Ai chỉ giúp mình câu này với!!!
Cho hàm số y= ax3 + bx2 + cx +d. Biết M(0;2), N(2;-2) là các điểm cực trị của đồ thị hàm số. Inhs giá trị của hàm số tại x=-2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 1 2019
Đáp án D
Ta có: Hàm số luôn đồng biến trên
ℝ ⇔ y ' = 3 a x 2 + 2 b x + c ≥ 0 ∀ x ∈ ℝ ⇔ a > 0 Δ y ' = b 2 − 3 a c ≤ 0
CM
30 tháng 8 2017
Đáp án B
Ta có
f ' x = 3 a x 2 + 2 b x + c ⇒ f ' 1 = 3 a + 2 b + c = 0 f ' − 1 = 3 a − 2 b + c = 0
Mặt khác
f 1 = a + b + c + d = − 1 f − 1 = − a + b − c + d = 3 ⇒ a = 1 ; b = 0 c = − 3 ; d = 1 ⇒ f x = x 3 − 3 x + 1 ⇒ f 4 = 53
CM
13 tháng 3 2017
Đáp án C
Phương trình có ba nghiệm phân biệt nếu y c t < m < y c d ⇔ - 2 < m < 2
CM
7 tháng 9 2017
Ta có thể vẽ đồ thị hàm số y = |ax3+ bx2+ cx+ d + 1| theo ba bước sau:
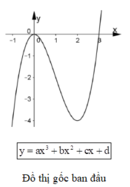
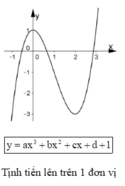
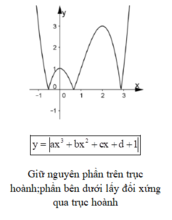
Dựa vào đồ thị ta thấy hàm số có 4 cực trị
Chọn C.
CM
26 tháng 7 2018
Chọn A
Ta có: f ' x = 3 a x 2 + 2 b x + c
có ∆ ' f ' x = b 2 - 3 a c .
Hàm số f x nghịch biến trên ℝ khi và chỉ khi
3 a < 0 ∆ ' f ' x ≤ 0
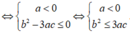
Lời giải:
\(y=ax^3+bx^2+cx+d\)
\(\Rightarrow y'=3ax^2+2bx+c\)
Vì $M(0;2)$ và $N(2;-2)$ là 2 điểm cực trị của đths đã cho nên \(x=0; x=2\) là 2 nghiệm của pt \(y'=3ax^2+2bx+c=0\)
Do đó:
\(\left\{\begin{matrix} 3a.0^2+b.0+c=0\\ 3a.2^2+2.b.2+c=0\end{matrix}\right.\) \(\Rightarrow \left\{\begin{matrix} c=0\\ 12a+4b=0\end{matrix}\right.(1)\)
Mặt khác, \(M(0;2); N(2;-2)\in (y)\) nên:
\(\left\{\begin{matrix} 2=a.0^3+b.0^2+c.0+d\\ -2=a.2^3+b.2^2+c.2+d\end{matrix}\right.\) \(\Rightarrow \left\{\begin{matrix} d=2\\ 8a+4b+2=-2\end{matrix}\right.(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=1\\ b=-3\\ c=0\\ d=2\end{matrix}\right.\)
Vậy $y=x^3-3x^2+2$
Suy ra \(y(-2)=-18\)
cho em hỏi đoạn cuối dùng công thức gì để tính ra abcd vậy ạ