Lập phương trình tiếp tuyến tại điểm \(M\left( { - {\rm{ }}1{\rm{ }};--4} \right)\) thuộc đường tròn\({\left( {x - 3} \right)^2} + {\left( {y + 7} \right)^2} = 25\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Phương trình tổng quát của đường thẳng\(\Delta \) đi qua điểm \(A\left( { - 1;{\rm{ }}2} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3{\rm{ }};{\rm{ }}2} \right).\)là: \(3\left( {x + 1} \right) + 2\left( {y - 2} \right) = 0 \Leftrightarrow 3x + 2y - 1 = 0\)
b) Do \(\Delta \) có vecto chỉ phương là \(\overrightarrow u = \left( { - 2{\rm{ }};{\rm{ 3}}} \right).\)nên vecto pháp tuyến của \(\Delta \) là \(\overrightarrow n = \left( {3{\rm{ }};{\rm{ }}2} \right).\)
Phương trình tổng quát của đường thẳng\(\Delta \) đi qua điểm \(A\left( { - 1;{\rm{ }}2} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3{\rm{ }};{\rm{ }}2} \right).\)là: \(3\left( {x + 1} \right) + 2\left( {y - 2} \right) = 0 \Leftrightarrow 3x + 2y - 1 = 0\)

a) Phương trình tổng quát của đường thẳng \({\Delta _1}\) là: \(2\left( {x - 1} \right) + 1\left( {y - 3} \right) = 0 \Leftrightarrow 2x + y - 5 = 0\).
b) Phương trình tham số của đường thẳng \({\Delta _2}\) là:\(\left\{ \begin{array}{l}x = - 2 + 3t\\y = 1 + 2t\end{array} \right.\)
c) Phương trình đường thẳng AB đi qua điểm \(A\left( {1;3} \right)\) nhận \(\overrightarrow {AB} = \left( { - 3; - 2} \right)\) là vectơ chỉ phương nên phương trình tham số của AB là \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 3 - 2t\end{array} \right.\)

a) Phương trình tổng quát của đường thẳng \(A{F_1}{\rm{ }}\)là:\(\frac{x}{{ - 3}} + \frac{y}{4} = 1 \Leftrightarrow 4x - 3y + 12 = 0\).
Phương trình tổng quát của đường thẳng \(A{F_2}{\rm{ }}\)là:\(\frac{x}{3} + \frac{y}{4} = 1 \Leftrightarrow 4x + 3y - 12 = 0\).
b) Giả sử tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = I{F_1} = I{F_2} \Leftrightarrow I{A^2} = I{F_1}^2 = I{F_2}^2\)
Vì \(I{A^2} = I{F_1}^2,I{F_1}^2 = I{F_2}^2\) nên: \(\left\{ \begin{array}{l}{a^2} + {\left( {4 - b} \right)^2} = {\left( { - 3 - a} \right)^2} + {b^2}\\{\left( { - 3 - a} \right)^2} + {b^2} = {\left( {3 - a} \right)^2} + {b^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = \frac{7}{8}\end{array} \right.\) .
=> \(I\left( {0;\frac{7}{8}} \right)\) và \(R = IA = \sqrt {{0^2} + {{\left( {\frac{{25}}{8}} \right)}^2}} = \frac{{25}}{8}\)
Vậy phương trình đường tròn ngoại tiếp tam giác \(A{F_1}{F_2}\) là: \({x^2} + {\left( {y - \frac{7}{8}} \right)^2} = {\left( {\frac{{25}}{8}} \right)^2}\)
c) Gọi phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\).
Do elip có 2 tiêu điểm \({F_1},{F_2}\) nên \(\sqrt {{a^2} - {b^2}} = c = 3 \Leftrightarrow {a^2} - {b^2} = 9\).
Mặt khác điểm A thuộc elip nên \(\frac{{16}}{{{b^2}}} = 1 \Leftrightarrow b = 4\left( {do{\rm{ }}b > 0} \right)\). Vậy \(a = 5\).
Vậy phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{{5^2}}} + \frac{{{y^2}}}{{{4^2}}} = 1\).

a) Tọa độ vecto pháp tuyến của \(\Delta \) là:
Tọa độ vecto chỉ phương của \(\Delta \) là:
b) Chọn \(x = 0;x = 1\) ta lần được được 2 điểm A và B thuộc đường thẳng \(\Delta \) là: \(A\left( {0;1} \right),B\left( {1;2} \right)\)

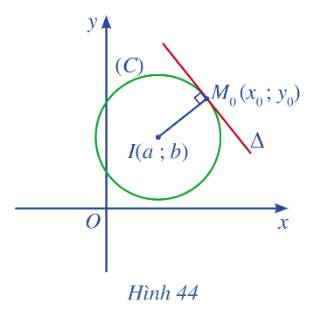
a) Do \(\Delta \) là pháp tuyến của đường tròn (C) tại điểm \({M_o}\) nên \(\Delta \) vuông góc với \(I{M_o}\). Vậy \(\overrightarrow {I{M_o}} \) là vectơ pháp tuyến của đường thẳng \(\Delta \).
b) Tọa độ \(\overrightarrow {I{M_o}} = \left( {{x_o} - a;{y_o} - b} \right)\)
c) Đường thẳng \(\Delta \)đi qua điểm \({M_o}\)và có vecto pháp tuyến \(\overrightarrow {I{M_o}} \)là: \(\left( {{x_o} - a} \right)\left( {x - {x_o}} \right) + \left( {{y_o} - b} \right)\left( {y - {y_o}} \right) = 0\)

a) Đường thẳng d đi qua hai điểm \(\left( { - 1;1} \right)\) và \(\left( {2;3} \right)\) nên phương trình đường thẳng d là: \(\frac{{x + 1}}{{2 + 1}} = \frac{{y - 1}}{{3 - 1}} \Leftrightarrow 2x - 3y + 5 = 0\)
b) Phương trình đường tròn (C) có tâm \(I\left( {2;1} \right)\) và \(R = 2\) là: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 4\)
c) Gọi \({d_1}\) là tiếp tuyến của đường tròn (C) tại điểm \(M\left( {2 + \sqrt 2 ;1 + \sqrt 2 } \right)\)
Ta có: \(\overrightarrow {{n_{{d_1}}}} = \overrightarrow {IM} = \left( {\sqrt 2 ;\sqrt 2 } \right)\). Vậy phương trình đường thẳng \({d_1}\) là:
\(\sqrt 2 \left( {x - 2 - \sqrt 2 } \right) + \sqrt 2 \left( {y - 1 - \sqrt 2 } \right) = 0 \Leftrightarrow x + y - 3 - 2\sqrt 2 = 0\)

Ta có: \(y'3x^2-3.2x=3x^2-6x\).
Tiếp tuyến với đồ thị của hàm số tại điểm \(M\left(-1;4\right)\) có hệ số góc bằng:\(y'\left(-1\right)=3.\left(-1\right)^2-6.\left(-1\right)=9\).
\(\Rightarrow B\)

a) Ta có: \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {HM} } \right|.\left| {\cos \left( {\overrightarrow n ,\overrightarrow {HM} } \right)} \right| = \sqrt {{a^2} + {b^2}} .HM.1 = \sqrt {{a^2} + {b^2}} .HM\)
b) Ta có : \(\overrightarrow n = \left( {{\rm{a }};{\rm{ b}}} \right)\left( {\overrightarrow n \ne 0} \right){\rm{ ,}}\overrightarrow {HM} = \left( {{x_1} - {x_o};{y_1} - {y_o}} \right) \Rightarrow \overrightarrow n .\overrightarrow {HM} = a\left( {{x_o} - {x_1}} \right) + b\left( {{y_o} - {y_1}} \right) = a{x_o} + b{y_o} + c\) trong đó \(a{x_1} + b{y_1} = c\).
c) Ta có: \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {HM} } \right|.\left| {\cos \left( {\overrightarrow n ,\overrightarrow {HM} } \right)} \right| \Leftrightarrow \left| {a{x_o} + b{y_o} + c} \right| = \sqrt {{a^2} + {b^2}} .HM \Rightarrow HM = \frac{{\left| {a{x_o} + b{y_o} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Đường tròn có tâm \(I\left( {3; - 7} \right)\).
Phương trình tiếp tuyến tại điểm \(M\left( { - {\rm{ }}1{\rm{ }};--4} \right)\) thuộc đường tròn \({\left( {x - 3} \right)^2} + {\left( {y + 7} \right)^2} = 25\) là: \(\left( { - 1 - 3} \right)\left( {x + 1} \right) + \left( { - 4 + 7} \right)\left( {y + 4} \right) = 0 \Leftrightarrow - 4\left( {x + 1} \right) + 3\left( {y + 4} \right) = 0 \Leftrightarrow - 4x + 3y + 8 = 0\)