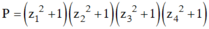Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Giả sử z = x + y i , x , y ∈ ℝ . Từ giả thiết ta có 2 x + y i − i = 2 + i x + y i
⇔ 2 x + 2 y − 1 i = 2 − y + x i ⇔ 4 x 2 + 2 y − 1 2 = y − 2 2 + x 2 ⇔ x 2 + y 2 = 1
Suy ra tập hợp các điểm A, B biểu diễn hai số phức z 1 , z 2 là đường tròn tâm O 0 ; 0 , bán kính R = 1 = O A = O B .
Giả sử z 1 = a 1 + b 1 i , z 2 = a 2 + b 2 i , a 1 , a 2 , b 1 , b 2 ∈ ℝ . Khi đó A a 1 ; b 1 , B a 2 ; b 2 .
Từ giả thiết z 1 − z 2 = 1 ta được:
a 1 − a 2 + b 1 − b 2 i = 1 ⇔ a 1 − a 2 2 + b 1 − b 2 2 = 1 ⇔ A B = 1
Từ đó O A = O B = A B ⇒ Δ O A B đều cạnh bằng 1.
Gọi M là trung điểm AB thì M a 1 + b 1 2 ; a 2 + b 2 2 và O M = A B 3 2 = 3 2 .
Khi đó
P = z 1 + z 2 = a 1 + a 2 + b 1 + b 2 i = a 1 + a 2 2 + b 1 + b 2 2
= 2 a 1 + a 2 2 2 + b 1 + b 2 2 2 = 2 O M = 2. 3 2 = 3
Chọn đáp án A
*Với z=0 thì phương trình đã cho trở thành 1=0 (Vô lý).
*Với z ≠ 0 ta chia cả hai vế của phương trình cho z 2 và được
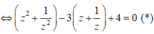
Phương trình (*) trở thành
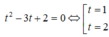
Vậy T = z 1 + z 2 + z 3 = 3
Đáp án C.
Ta có:
z = r c o s φ + s i n φ ⇒ z 2 = r 2 c o s 2 φ + i s i n 2 φ
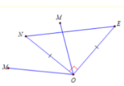
Gọi M z 1 ; n i z 2 ; E z 2 ta có: N O E ^ = 90 °
Do M O N ^ = 60 ° ⇒ M O E ^ = 30 ° M O E ^ = 150 °
Ta có z 1 2 = 36 ∠ 2 φ 1 ; 9 z 2 2 = 36 ∠ 2 φ 2
Do đó z 1 2 + 9 z 2 2 là độ dài của tổng 2 vecto chung gốc O có độ dài lần lượt là: 36 và 36 và góc giữa 2 vecto đó là 2 M O E ^ .
Suy ra
S 2 = 36 2 + 36 2 + 2.36.36. cos 2 M O E ^ ⇒ S 2 = 3888 ⇒ S = 36 3
Đáp án C.
Ta có 1 = z 1 - z 2 z 1 - z 2 = z 1 - z 2 z 1 - z 2 ¯ = z 1 2 + z 2 2 - z 1 z 2 + z 2 z 1 ⇔ z 1 z 2 + z 2 z 1 = 1 P = z 1 z 2 2 + z 2 z 1 2 = z 1 z 2 + z 2 z 1 2 - 2 = z 1 z 2 z 2 2 + z 2 z 1 z 1 2 2 - 2 = z 1 z 2 + z 2 z 1 2 - 2 = - 1 . .
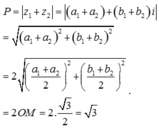
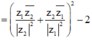
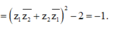
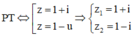
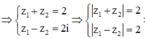
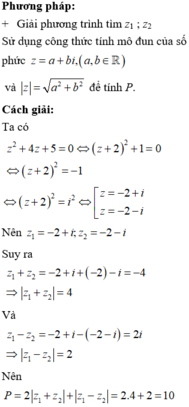
Chọn B.
Phương trình đã cho tương đương với ( -3z2 + 2iz = 0 ( 1) hoặc 5z2 - 6iz - 2 = 0 ( 2)
Giải : ta có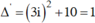
Suy ra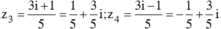
Do đó: