Tìm số phức z thỏa mzãn hệ thức z - 2 + i = 10 và z . z ¯ = 25
A. z = 3 + 4i; z = 5.
B. z = 3 + 4i; z = -4.
C. z = -3 + 4i; z = 5.
D. z = 3 - 4i; z = -5.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
![]()
⇒ z ¯ = a - b i

![]()
![]()
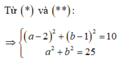
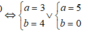
Vậy có hai số phức thỏa mãn là: z = 3+ 4i hoặc z = 5.

Chọn A.
Gọi M( x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.
Biểu diễn hình học của P là đường thẳng và P = 4x + 2y + 3.
Áp dụng bất đẳng thức Bunyakovsky ta có:
P = 4x + 2y + 3 = 4(x – 3) + 2(y – 4) + 23
![]()
Vậy MaxP = 33 

Đặt z = x + yi. Từ điều kiện của đầu bài ta được:
x - 2 2 + y - 1 2 = 10 và x 2 + y 2 = 25
Đáp số: z = 5 và z = 3 + 4i

Đặt z = x + yi. Từ điều kiện của đầu bài ta được:
( x - 2 ) 2 + ( y - 1 ) 2 = 10 và x 2 + y 2 = 25
Đáp số: z = 5 và z = 3 + 4i

Chọn B.
Giả sử z = x + yi. Theo bài ra ta có: |x + 1 + (y – 2)i| = |x + 3 + (4 – y)i|
hay ( x + 1) 2+ ( y - 2) 2 = ( x + 3) 2 + ( y - 4) 2
suy ra y = x + 5
Số phức
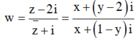
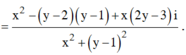
w là một số ảo
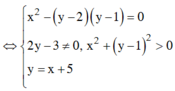
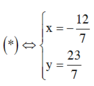
Vậy 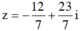
Chọn A.
Gọi z = a + bi khi đó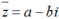
Hay (a – 2)2 + (b – 1)2 = 10
Từ (*) và (**)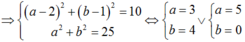
Vậy z = 3 + 4i hoặc z = 5.