Cho hai số phức . Gọi a là phần thực và b là phần ảo của số phức . Mệnh đề nào dưới đây đúng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(z_1-z_2=1+i-\left(3-7i\right)=1+i-3+7i=-2+8i\)
\(\Rightarrow\left|z_1+z_2\right|=\sqrt{\left(-2\right)^2+8^2}=2\sqrt{17}\)

Chọn đáp án A
Ta có w = z - z ' = 4 + 3 i
⇒ w = 4 2 + 3 2 = 5

Chọn đáp án B
Gọi các kích thước của khối hộp là a (cm), b(cm), c (cm) với a, b, c là các số nguyên dương.
Từ giả thiết ta có
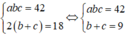
Lại có 9 = b + c ≥ 2 b c ⇒ b c ≤ 81 4
Mà b, c là các số nguyên dương nên b c ≤ 20
Từ b +c =9
⇒ trong hai số b, c có 1 số lẻ và 1 số chẵn ⇒ bc chẵn.
Từ a = 42 b c và a nguyên dương nên bc là ước nguyên dương của 42.

Nếu bc =6 thì b, c là nghiệm của phương trình X 2 - 9 X + 6 = 0 (loại vì nghiệm của phương trình này không là số nguyên).
Nếu bc =14 thì b, c là nghiệm của phương trình
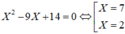
⇒ b c = 14 thỏa mãn. Vậy chiều cao của khối hộp là a = 42 b c = 3 c m

Chọn B.
Ta có z = z1.z2 = (1 + i) .(1 - 2i) = 1 - 2i + i - 2i2 = 3 - i.

Chọn A.
Ta có z = (1 + i)2 (4 - i) = (1 + 2i + i2)(4 - i) = 2i.(4 - i) = 8i - 2i2 = 2 + 8i.

Chọn D.
Giả sử z=a+bi với a,b ∈ ℝ
Thay vào biểu thức ta được:
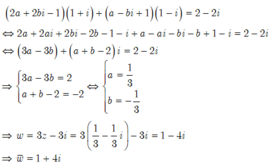

Chọn A. Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = 1 + i. Do đó:
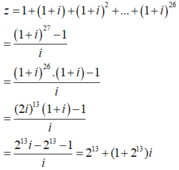
Vậy phần thực là: 213

Chọn đáp án D