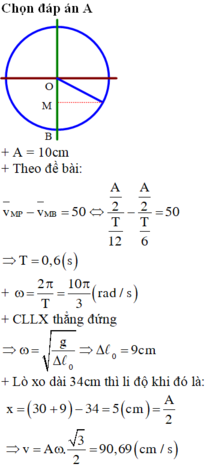b) Tìm điểm Mo (xo ; yo) thuộc đồ thị hàm số y=\(\frac{-2}{3}\)x biết: 5yo+2\(\left|x_o\right|\)=8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
24 tháng 12 2017
Chọn A
+ Động năng bằng thế năng ở vị trí x = ±A√2/2 = ±√2 cm và v = ωA/√2 = 6π cm.
+ Khi mo rơi và dính vào m, theo định luật bảo toàn động lượng (chú ý là vật m0 rơi thẳng đứng nên động lượng của nó theo phương ngang = 0): (m+mo)v’ = mv => v’ = 4π cm/s.
+ Hệ (m + mo) có ω’ = 2π√3 rad/s và qua VTCB vận tốc của hệ là:
CM
5 tháng 4 2019
Phương trình tiếp tuyến của đồ thị (C) của hàm số y = f(x) tại điểm Mo (xo;f(xo )) có dạng : y = f’(xo)(x – xo) + yo, trong đó yo = f(xo).
CM
3 tháng 9 2017
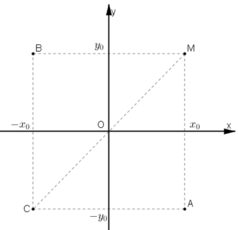
Biểu diễn các điểm trên hệ trục tọa độ ta thấy:
a) Điểm đối xứng với M(x0; y0) qua trục Ox là A(x0 ; –y0)
b) Điểm đối xứng với M(x0 ; y0) qua trục Oy là B(–x0 ; y0)
c) Điểm đối xứng với M(x0 ; y0) qua gốc O là C(–x0 ; –y0).
TT
0
CM
4 tháng 6 2019
TXĐ: D = R.
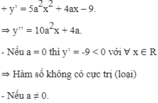
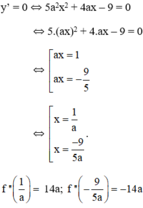
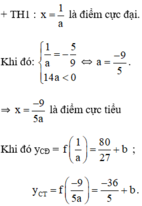
Các cực trị của hàm số đều dương
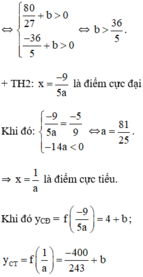
Các cực trị của hàm số đều dương
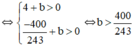
Vậy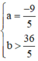 
hoặc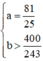 
là các giá trị cần tìm.
LA
27 tháng 6 2018
Đề phải là: Một con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể, độ cứng k = 50(N/m); khối lượng vật treo m = 200g. Vật đang đứng yên ở vị trí cân bằng thì được kéo thẳng đứng xuống dưới để lò xo giãn tổng cộng 12cm rồi thả cho nó dao động điều hòa. Lấy \(\pi^2=10;g=10\left(m,s^2\right)\). Trong một chu kỳ dao động thời gian lực đàn hồi tác dụng vào vật cùng chiều với lực hồi phục là:
Ta có: \(T=2\pi\sqrt{\dfrac{m}{k}}=0,4s\)
Tại VTCB lò xo giãn 1 đoạn bằng: \(\Delta l=\dfrac{mg}{k}=0,04m=4cm\)
Kéo thẳng đứng xuống dưới để lò xo giãn tổng cộng 12cm rồi thả cho nó dao động điều hòa =>A = 12 - 4 = 8 cm.
Trong một chu kỳ dao động thời gian lực đàn hồi tác dụng vào vật cùng chiều với lực hồi phục là:
t=T/2+T/3=5T/6=1/3s