tìm đạo hàm cấp n của hàm y=cosx; y=tanx; y=cotx; y=sinx.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mình tìm thấy nguồn này nhưng cách làm này không đúng nhé nên mình mới đăng câu hỏi để hỏi m.n

Đáp án A
y ' = e x sin x − cos x ' = e x sin x − cos x + e x sin x + cos x y ' = 2 e x . sin x

Đáp án C.
Viết lại dưới dạng y = cos x − 3 3 4 x
⇒ y ' = cos x − 3 ' .3 4 x − cos x − 3 . 3 4 x ' 3 4 x 2
y ' = − sin x .3 4 x − cos x − 3 .4 3 4 x ln 3 3 4 x 2 = − sin x − cos x − 3 .4 ln 3 3 4 x

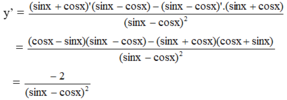
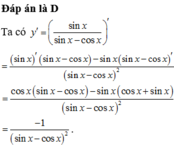
\(y=sinx\Rightarrow y'=cosx;y''=-sinx;y'''=-cosx\)
Bằng quy nạp toán học ; ta c/m được : \(y^{\left(n\right)}sinx=sin\left(x+n\dfrac{\pi}{2}\right)\)