Tìm m để ba đường thẳng y = 2x – 3 (d1); y = x – 1 (d2); y = (m − 1)x + 2 (d3) đồng quy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Hoành độ giao điểm của d 1 và d 2 là nghiệm phương trình:
2x + 1 = x -1 nên x = -2
Với x = -2 thì y = 2. (-2) + 1 = -3
Vậy 2 đường thẳng d 1 và d2 cắt nhau tại A(-2; -3).
Để ba đường thẳng đã cho đồng quy thì điểm A(-2; -3) thuộc đồ thị hàm số y = (m + 1)x – 2
Suy ra: -3 = (m + 1).(-2) - 2
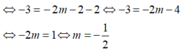

1: Để hai đường song song thì m+3=2
hay m=-1
3: Tọa độ của điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\2x+4=0\end{matrix}\right.\Leftrightarrow A\left(-2;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}y_B=0\\-x+4=0\end{matrix}\right.\Leftrightarrow B\left(4;0\right)\)

Bài 3:
Vì (d)//(d1) nên a=3
Vậy: (d): y=3x+b
Thay \(x=\dfrac{2}{3}\) và y=0 vào (d), ta được:
\(b+2=0\)
hay b=-2

a, để (d2)//(d3)
\(< =>\left\{{}\begin{matrix}m^2+1=2\\m\ne1\end{matrix}\right.\)\(< =>m=-1\)
b, pt hoành độ giao điểm (d1)(d2)
\(x+2=2x+1< =>x=1=>y=3\)
\(pt\) hoành độ (d2)(d3)
\(2x+1=\left(m^2+1\right)x+m< =>2+1=\left(m^2+1\right)2+m\)
\(=>m=0,5\)

a) Phương trình hoành độ giao điểm của d₁ và d₂
x + 2 = 5 - 2x
⇔ x + 2x = 5 - 2
⇔ 3x = 3
⇔ x = 1
Thay x = 1 vào d₁ ta có:
y = 1 + 2 = 3
⇒ Giao điểm của d₁ và d₂ là A(1; 3)
Thay tọa độ điểm A vào d₃ ta có:
VT = 3
VP = 3.1 = 3
⇒ VT = VP
Hay A ∈ d₃
Vậy d₁, d₂ và d₃ đồng quy
b) Thay tọa độ điểm A(1; 3) vào d₄ ta có:
m.1 + m - 5 = 3
⇔ 2m - 5 = 3
⇔ 2m = 3 + 5
⇔ 2m = 8
⇔ m = 8 : 2
⇔ m = 4
Vậy m = 4 thì d₁, d₂ và d₄ đồng quy

Tọa độ giao điểm của (d1) và (d2) là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}2x+1=x+2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-x=2-1\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
Để (d1),(d2),(d3) đồng quy thì (d3) đi qua A(1;3)
Thay x=1 và y=3 vào (d3), ta được:
\(m^2+1+m=3\)
=>\(m^2+m-2=0\)
=>\(m^2+2m-m-2=0\)
=>\(\left(m+2\right)\left(m-1\right)=0\)
=>\(\left[{}\begin{matrix}m+2=0\\m-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-2\\m=1\end{matrix}\right.\)
 help me pls
help me pls
Đáp án D