Các đường thẳng y = −5(x + 1); y = 3x + a; y = ax + 3 đồng quy với giá trị của a là
A. −13 hoặc 3
B. 13 hoặc −3
C. −12
D. −13
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(d1): 2x + y - 3 = 0
y = -2x + 2
(d2): y = 5 - 2x
y = -2x + 5
(d3): 2y = x + 4
y = x/2 + 2
(d4): x + y - 1 = 0
y = -x + 1
*) Cặp đường thẳng song song:
(d1) và (d2)
*) Các cặp đường thẳng cắt nhau:
(d1) và (d3); (d1) và (d4); (d2) và (d3); (d2) và (d4); (d3) và (d4)

\(\left(1\right)\cap\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5\ne2m+1\\-2m+3\ne3m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne4\\m\ne\dfrac{3}{5}\end{matrix}\right.\\ \left(1\right)//\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5=2m+1\\-2m+3\ne3m\end{matrix}\right.\Leftrightarrow m=4\\ \left(1\right)\equiv\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
a). Để hai hàm số cắt nhau thì:
a≠a'⇒ m+5=2m+1
⇔ m+5=2m+1
⇔ m-2m=1-5
⇔ -m = -4
⇔ m = 4.
Vậy hai hàm số cắt nhau khi m =4.
b). Để hai hàm số song song khi:
\(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}m=-4\\m\ne\dfrac{3}{5}\end{matrix}\right.\)
Vậy hai hàm số đó song song khi m=-4; m≠\(\dfrac{3}{5}\).
c). Để hai hàm số trùng nhau khi:
\(\left\{{}\begin{matrix}a=a'\\b=b'\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}m=-4\\m=\dfrac{3}{5}\end{matrix}\right.\)
Vậy hai hàm số đó trùng nhau khi m=-4; m=\(\dfrac{3}{5}\).

a: Phương trình hoành độ giao điểm là:
-3x-3=-2x
=>-3x+2x=3
=>-x=3
=>x=-3
Thay x=-3 vào y=-2x, ta được:
\(y=-2\cdot\left(-3\right)=2\cdot3=6\)
Vậy: Hai đường thẳng y=-3-3x và y=-2x cắt nhau tại điểm A(-3;6)
b: Phương trình hoành độ giao điểm là:
\(3\left(x-1\right)-5x=-\sqrt{5}\cdot x-2\)
=>\(-2x-3=-\sqrt{5}\cdot x=-2\)
=>\(-2x+x\cdot\sqrt{5}=-2+3=1\)
=>\(x\left(\sqrt{5}-2\right)=1\)
=>\(x=\dfrac{1}{\sqrt{5}-2}=\sqrt{5}+2\)
Thay \(x=\sqrt{5}+2\) vào y=3(x-1)-5x, ta được:
\(y=3x-3-5x=-2x-3=-2\cdot\left(\sqrt{5}+2\right)-3\)
\(=-2\sqrt{5}-4-3=-2\sqrt{5}-7\)
Vậy: Tọa độ giao điểm của hai đường thẳng \(y=-x\sqrt{5}-2;y=3\left(x-1\right)-5x\) là \(B\left(\sqrt{5}+2;-2\sqrt{5}-7\right)\)

+ Phương trình hoành độ giao điểm giữa hai đường thẳng y= -5( x+ 1) và y=3x+a :
-5x-5=3x+a suy ra -8x-a=5 (1)
+ Phương trình hoành độ giao điểm giữa hai đường thẳng y= 3x+a và y=ax+3là:
ax+3=3x+a hay (a-3) x=a-3
suy ra x=1( vì a≠3).
+Thế x= 1 vào (1) ta được: -8-a=5 nên a= -13.
Chọn D.

a:
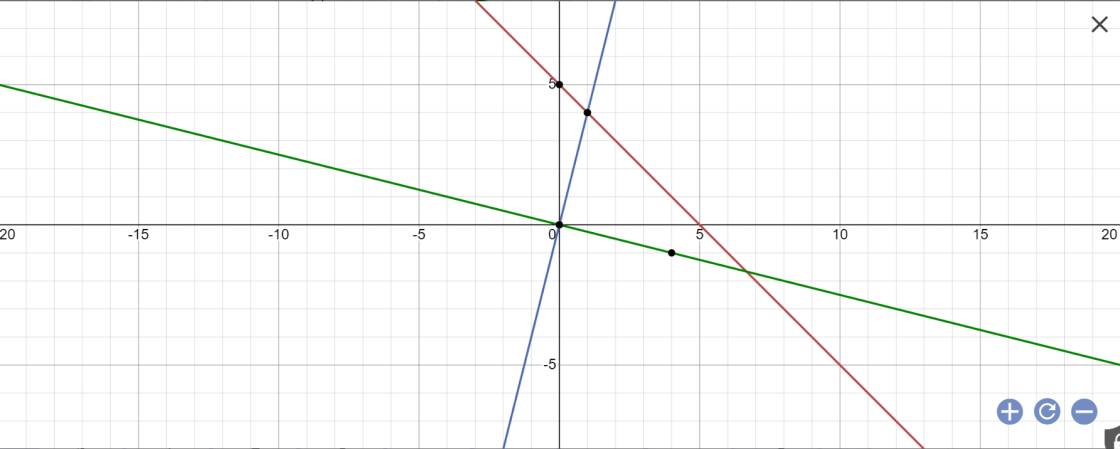
b: tọa độ A là;
-x+5=4x và y=4x
=>x=1 và y=4
Tọa độ B là;
-x+5=-1/4x và y=-1/4x
=>-3/4x=-5 và y=-1/4x
=>x=5:3/4=5*4/3=20/3 và y=-1/4*20/3=-5/3
=>B(20/3;-5/3)
c: O(0;0); A(1;4); B(20/3;-5/3)
\(OA=\sqrt{1^2+4^2}=\sqrt{17}\)
\(OB=\sqrt{\left(\dfrac{20}{3}\right)^2+\left(-\dfrac{5}{3}\right)^2}=\dfrac{5\sqrt{17}}{3}\)
\(AB=\sqrt{\left(\dfrac{20}{3}-1\right)^2+\left(-\dfrac{5}{3}-4\right)^2}=\dfrac{\sqrt{818}}{3}\)
\(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{-8}{17}\)
=>góc AOB tù
=>ΔOAB tù

đường thẳng y = ax+ b song song với đường thằng y = -x+ 5
=> a = -1 ; b khác 5
=> đường thẳng có dạng y = -x + b
gọi A là giao của đg thẳng y = -x + b và parabol
=> xA = 1 => yA = xA2 = 1
A(1; 1) thuộc đg thẳng y = -x + b => yA = - xA + b =>b = 2 (thoả mãn)
Đáp án D