tính giá trị biểu thức
x2 - 2xy + y2 tại x = 11 ; y = 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 7 2021
Biểu thức này không tồn tại cả GTNN và GTLN
(Muốn tồn tại GTLN thì hệ số của cả \(x^2\) và \(y^2\) đều phải âm, trong khi bài này hệ số của \(x^2\) dương)
18 tháng 10 2021
\(a,A=\left(x+y\right)^2-9z^2=\left(x+y-3z\right)\left(x+y+3z\right)\\ A=\left(5+7-36\right)\left(5+7+36\right)=-24\cdot48=-1152\\ b,B=\left(2x-y\right)\left(2x+y\right)+\left(2x+y\right)=\left(2x+y\right)\left(2x-y-1\right)\\ B=\left(2+2\right)\left(2-2-1\right)=4\cdot\left(-1\right)=-4\)
5N
1
12 tháng 11 2021
\(=\left(x-y\right)^2+x=\left(25-5\right)^2+5=20^2+5=405\)
25 tháng 12 2021
\(a,=5\left(x^2+2xy+y^2\right)-10y^2+5=5\left(x+y\right)^2-10y^2+5\\ =5\left(1+2\right)^2-10\cdot4+5=45-40+5=10\\ b,=7\left(x-y\right)-\left(x-y\right)^2=\left(x-y\right)\left(7-x+y\right)\\ =\left(2-2\right)\left(7-2+2\right)=0\)
25 tháng 12 2021
b: \(=7\left(x-y\right)-\left(x-y\right)^2\)
\(=\left(x-y\right)\left(7-x+y\right)=0\)
NH
2
11 tháng 8 2021
a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)
\(=\left(x-y\right)^2-10\left(x-y\right)\)
\(=9^2-10\cdot9=-9\)
1 tháng 11 2023
a: \(N=\left(2x-3y\right)\left(2x+3y\right)=\left(2x\right)^2-\left(3y\right)^2\)
\(=4x^2-9y^2\)
Thay x=1/2 và y=1/3 vào N, ta được:
\(N=4\cdot\left(\dfrac{1}{2}\right)^2-9\left(\dfrac{1}{3}\right)^2\)
\(=4\cdot\dfrac{1}{4}-9\cdot\dfrac{1}{9}\)
=1-1
=0
b: \(N=\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
\(=\left(2x-y\right)\left[\left(2x\right)^2+2x\cdot y+y^2\right]\)
\(=\left(2x\right)^3-y^3=8x^3-y^3\)
Khi x=1 và y=3 thì \(N=8\cdot1^3-3^3=8-27=-19\)
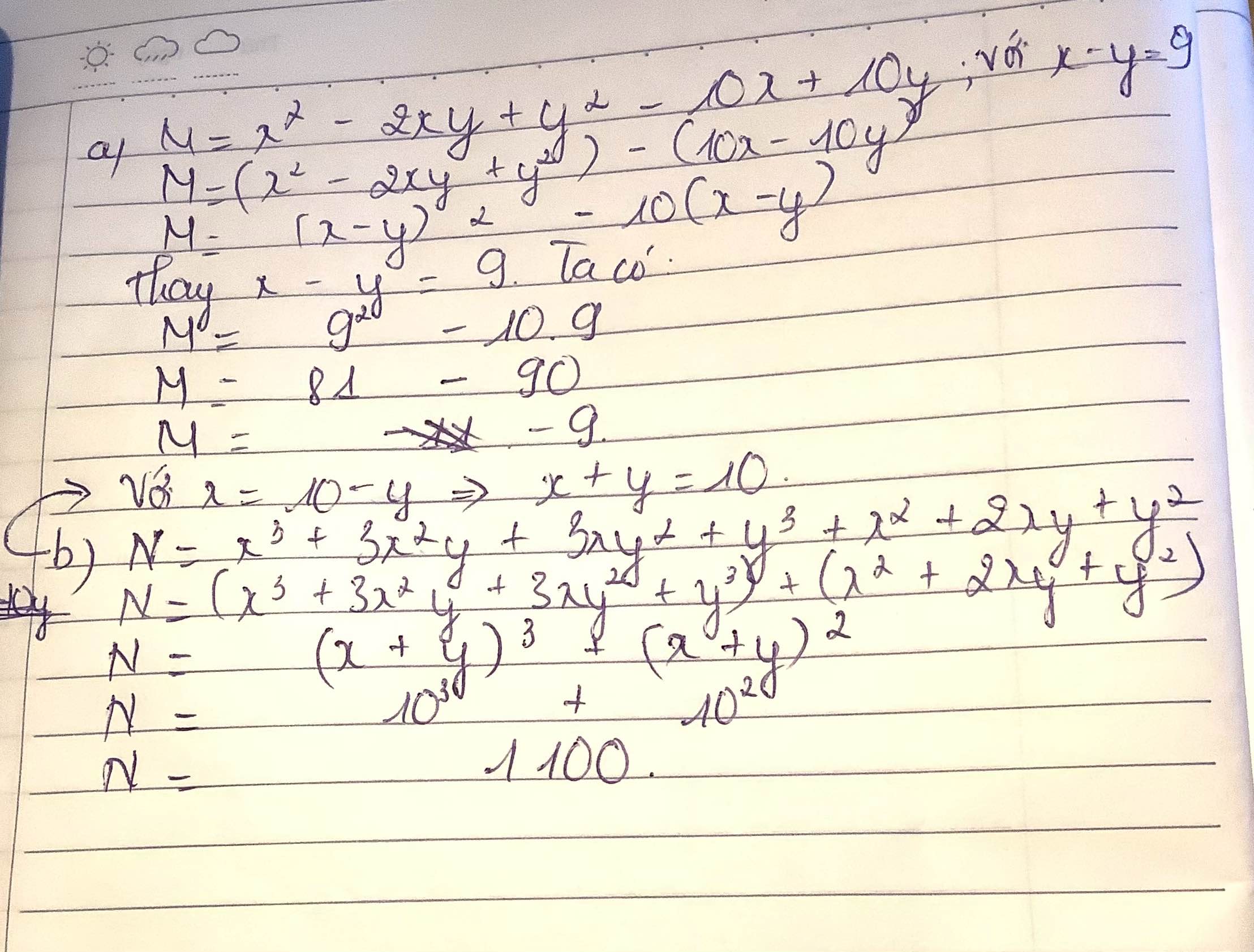
\(A=x^2-2xy+y^2=\left(x-y\right)^2\)
Khi x=11 và y=1 thì \(A=\left(11-1\right)^2=10^2=100\)
`x^2-2xy+y^2`
`=(x-y)^2`
Tại `x=11;y=1`
Ta có : `(x-y)^2 = (11-1)^2=10^2=100`