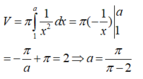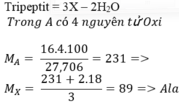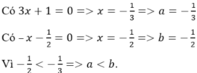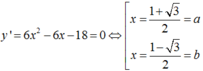Gọi A x 1

PT

Pham Trong Bach

26 tháng 1 2017

Gọi A x 1 ; y 1 , B x 2 ; y 2 là hai điểm cực trị của đồ thị hàm số y = x 3 - 3 x - 2 . Giá trị y 1 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

26 tháng 1 2017

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

19 tháng 9 2023

a) Gọi x là số làm tròn đến hàng chục của số a=3128. Hãy chứng tỏ:

\(\left| {a - x} \right| \le 5\) và \(x - 5 \le a \le x + 5\)

b) Gọi y là số làm tròn đến hàng phần trăm của \(\frac{1}{3}\). Hãy chứng tỏ \(\left| {\frac{1}{3} - y} \right| \le 0,005\).

#Hỏi cộng đồng OLM #Toán lớp 7

1

HQ

Hà Quang Minh

Giáo viên

19 tháng 9 2023

a)

+) Ta có: a=3128 suy ra \(x = 3130\).

\(\left| {a - x} \right| = \left| {3128 - 3130} \right| = \left| { - 2} \right| = 2 \le 5\)

Vậy \(\left| {a - x} \right| \le 5\).

+) Ta có:

\(\begin{array}{l}x - 5 = 3128 - 5 = 3123\\x + 5 = 3128 + 5 = 3133\end{array}\)

Nên \(x - 5 \le a \le x + 5\)

b) Do y là số làm tròn đến hàng phần trăm của \(\frac{1}{3}\) nên \(y = 0,33\).

Ta có: \(\left| {\frac{1}{3} - y} \right| = \left| {\frac{1}{3} - 0,33} \right| = \left| {\frac{1}{{300}}} \right| = \frac{1}{{300}} = 0,00\left( 3 \right) \le 0,005\).

Nên \(\left| {\frac{1}{3} - y} \right| \le 0,005\).

Đúng(0)

P

~P.T.D~

13 tháng 2 2023

Gọi `bb A` là giới hạn của hàm số `f(x)=[x+x^2+x^3+...+x^50 -50]/[x-1]` khi `x -> 1.` Tính giá trị của `bb A.`

#Hỏi cộng đồng OLM #Toán lớp 11

0

NL

Nanami Luchia

3 tháng 1 2017

1. Gọi x là tổng các.chức số a = 3^2010+2011 gọi y là tổng các chữ số của x, gọi z là tổng các chữ số của y. Tìm z

2. Tìm x £ N

a) 41— 2^x—1=9

b) |x—3|—21= _5

d) 6M+7= 7^x+1 với M = 7+7^2+7^3+...+7^2016

g) x+9 chia hết x—2

3. Tìm x, y biết:

a) ( x + 1)^100+|y—3| =0

#Hỏi cộng đồng OLM #Toán lớp 6

2

NH

Nguyễn Huy Tú

3 tháng 1 2017

Bài 2:
\(41-2^x-1=9\)

\(\Rightarrow40-2^x=9\)

\(\Rightarrow2^x=31\)

\(\Rightarrow x\in\left\{\varnothing\right\}\)

Vậy không có giá trị x thỏa mãn

b) \(\left|x-3\right|-21=-5\)

\(\Rightarrow\left|x-3\right|=16\)

\(\Rightarrow x-3=\pm16\)

+) \(x-3=16\Rightarrow x=19\)

+) \(x-3=-16\Rightarrow x=-13\)

Vậy \(x\in\left\{19;-13\right\}\)

d) Ta có: \(M=7+7^2+...+7^{2016}\)

\(\Rightarrow7M=7^2+7^3+...+7^{2017}\)

\(\Rightarrow7M-M=\left(7^2+7^3+...+7^{2017}\right)-\left(7+7^2+...+7^{2016}\right)\)

\(\Rightarrow6M=7^{2017}-7\)

\(6M+7=7^{x+1}\)

\(\Rightarrow7^{2017}-7+7=7^{x-1}\)

\(\Rightarrow7^{x-1}=7^{2017}\)

\(\Rightarrow x-1=2017\)

\(\Rightarrow x=2018\)

Vậy \(x=2018\)

g) Ta có: \(x+9⋮x-2\)

\(\Rightarrow\left(x-2\right)+11⋮x-2\)

\(\Rightarrow11⋮x-2\)

\(\Rightarrow x-2\in\left\{1;-1;11;-11\right\}\)

+) \(x-2=1\Rightarrow x=3\)

+) \(x-2=-1\Rightarrow x=1\)

+) \(x-2=11\Rightarrow x=13\)

+) \(x-2=-11\Rightarrow x=-9\)

Vậy \(x\in\left\{3;1;13;-9\right\}\)

Bài 3:

a) \(\left(x+1\right)^{100}+\left|y-3\right|=0\)

\(\Rightarrow\left(x+1\right)^{100}=0\) và \(\left|y-3\right|=0\)

+) \(\left(x+1\right)^{100}=0\Rightarrow x+1=0\Rightarrow x=-1\)

+) \(\left|y-3\right|=0\Rightarrow y-3=0\Rightarrow y=3\)

Vậy \(x=-1;y=3\)

Đúng(0)

NL

Nanami Luchia

3 tháng 1 2017

Giúp mình với

Đúng(0)

NB

Người Bí Ẩn

23 tháng 1 2024

Gọi A là giao điểm của 2 đường thẳng y=-x+1 và y=x+3. Tìm số nguyên dương m để A thuộc đồ thị hàm số y = (m-1)x+m^2-1

#Hỏi cộng đồng OLM #Toán lớp 9

1

NV

Nguyễn Việt Lâm

Giáo viên

23 tháng 1 2024

Pt hoành độ giao điểm:

\(-x+1=x+3\Rightarrow2x=-2\)

\(\Rightarrow x=-1\Rightarrow y=x+3=2\)

\(\Rightarrow A\left(-1;2\right)\)

Để A thuộc \(y=\left(m-1\right)x+m^2-1\) thì:

\(-1.\left(m-1\right)+m^2-1=2\)

\(\Leftrightarrow m^2-m-2=0\Rightarrow\left[{}\begin{matrix}m=-1\left(loại\right)\\m=2\end{matrix}\right.\)

Đúng(2)

PT

Pham Trong Bach

10 tháng 9 2018

Gọi V là thể tích của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = 1/x, y=0, x=1, x=a, a>1. Tìm a để V = 2. ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

10 tháng 9 2018

Đáp án A

Đúng(0)

NH

Nguyễn Hoàng Nam

20 tháng 5 2017

Tripeptit A chỉ tạo bởi aminoaxit no X ( X có 1 nhóm NH₂ và 1 nhóm COOH). Phần trăm khối lượng của oxi trong A là 27,706%. Tên gọi tắt của X là

A. Ala

B. Gly

C. Glu

D. Val

#Hỏi cộng đồng OLM #Mẫu giáo

1

NQ

Ngô Quang Sinh

20 tháng 5 2017

Chọn A

Đúng(0)

PT

Pham Trong Bach

9 tháng 4 2017

Gọi a là nghiệm của đa thức f ( x ) = 3 x + 1 , b là nghiệm của đa thức g ( x ) = - x - 1 / 2 . Kết luận nào sau đây là đúng về a và b A. a > b B. a < b C. a = b D. Không kết luận được...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

1

CM

Cao Minh Tâm

9 tháng 4 2017

Chọn A

Đúng(0)

PT

Pham Trong Bach

28 tháng 6 2018

Gọi x = a và x = b là các điểm cực trị của hàm số y = 2x³ – 3x² – 18x - 1. Khi đó A = a + b – 2ab bằng:

A. -7

B. 5

C. 7

D. -5

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

28 tháng 6 2018

Chọn C.

Suy ra A = a + b - 2ab = 7.

Đúng(0)

N

nguyenhoang

16 tháng 4 2020 - olm

1) Cho biểu thức A = (2x/x-3-3x^2+3/x^2-9+x/x+3).x+3/x-1)a) Tìm điều kiện của x để biểu thức A xác định.b) Rút gọn A.c) Tìm x để biểu thức A có giá trị bằng 3.2) x(2-5x)=4(x-1)3) Cho tam giác ABC vuông ở A. Gọi M, N lần lượt là trung điểm của các cạnh AB và BC. Gọi P là điểm đối xứng của M qua điểm N.a)Tính diện tích của tam giác ABC khi AB =6cm, AC = 10cm.b) Tứ giác MBPC là hình bình hành?Vì sao?c)...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 8

0

LT

Lê Thị Phương Uyên

10 tháng 1 2023 - olm

A gọi B bằng bác , B gọi C là ông nội ,C gọi D là cậu , D gọi E là gì ,E gọi F là chú , F gọi Z là con , Z gọi X là bố , X gọi V là cụ , V gọi M là chồng . hỏi A gọi M là gì .

#Hỏi cộng đồng OLM #Toán lớp 6

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP