Cho x>0; y>0 và 2x+3y\(\le\) 2. Tìm GTNN của \(A=\frac{4}{4x^2+9y^2}+\frac{9}{xy}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét hiệu: (x+y)(y+z)(z+x)-8xyz=0
(=) (x+y)>=2√xy
(y+z)>=2√yz
(z+x)>=2√zx
(=) (x+y)(y+z)(z+x)>=8√x^2 y^2 z^2
(=) (x+y)(y+z)(x+z)>=8|x| |y| |z|
(=) ( x+y)(y+z)(z+x)>= 8xyz

Lời giải:
Nếu $x>0$ thì $-x< 0$. Do đó $-x< 0< x\Rightarrow -x< x$. Đáp án A sai
Nếu $x>0\Rightarrow -x< 0$. Đáp án B sai
Nếu $x< 0\Rightarrow -x>0$. Do đó $-x>0>x\Rightarrow -x>x$. Đáp án C sai
Nếu $x>0\Rightarrow -x< 0$. Đáp án D đúng (chọn)

vì x,y,z>0 nên áp dụng bđt côsi ta có
x+y >= 2\(\sqrt{xy}\)
y+z >= 2\(\sqrt{yz}\)
z+x >= 2\(\sqrt{xz}\)
\(\Rightarrow\)(x+y)(y+z)(z+x) >= 8\(\sqrt{x^2y^2z^2}\)
>= 8xyz
Dấu = xảy ra <=> x=y=z

Ta có:
\(\frac{x}{x+1}=1-\frac{1}{x+1}\)
\(\frac{y}{y+1}=1-\frac{y}{y+1}\)
\(\frac{z}{z+4}=1-\frac{4}{z+4}\)
\(\Rightarrow\frac{x}{x+1}+\frac{y}{y+1}+\frac{z}{z+4}=3-\left(\frac{1}{x+1}+\frac{1}{y+1}+\frac{4}{z+4}\right)\)
\(\le\left[3-\left(\frac{4}{x+y+2}+\frac{4}{z+4}\right)\right]\le\left(3-\frac{16}{x+y+z+6}\right)=3-\frac{16}{6}=\frac{1}{3}\)

Ta có x. (-x)=x.x.(-1)=-x^2>0
==> x^2<0 (vì âm của nó là dương) (1)
mà x>0==>x^2>0 (2)
Từ (1) và (2) ==> mâu thuẫn
Vậy x thuộc rỗng



\(2\ge2x+3y\ge2\sqrt{2x.3y}\Rightarrow xy\le\frac{1}{6}.\)
\(A=\frac{4}{4x^2+9y^2}+\frac{9}{xy}=\frac{4}{4x^2+9y^2}+\frac{4}{12xy}+\frac{26}{3xy}\ge\frac{\left(2+2\right)^2}{4x^2+9y^2+12xy}+\frac{26}{3xy}\)
\(\ge\frac{4^2}{2^2}+\frac{26}{3.\frac{1}{6}}=56\)
Dấu \(=\)khi \(\hept{\begin{cases}\frac{2}{4x^2+9y^2}=\frac{2}{12xy}\\2x=3y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{1}{3}\end{cases}}\)
Áp dụng bất đẳng thức Cô – si cho hai số dương, ta có: 2x + 3y ≥ 2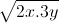
⇔ 2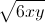 ≤ 2x + 3y
≤ 2x + 3y
Mà 2x + 3y ≤ 2
Do đó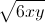 ≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
A =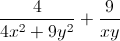 = 4(
= 4(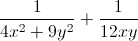 ) +
) + 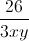 ≥ 4
≥ 4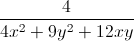 +
+ 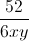 = 16
= 16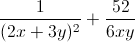 ≥ 16.
≥ 16.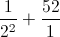 = 56
= 56
Dấu “ = “ xảy ra ⇔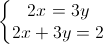 ⇔
⇔ 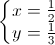
Vậy giá trị nhỏ nhất của biểu thức A là 56.