x/4=y/3 ; y/5=z/6 và x+y-z=49
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đối với các câu này bạn hãy khai triển phần nào dài bằng hàng dẳng thức rồi thu gọn lại nếu đúng thì vế trái bằng vế phải

Sửa đề: Các dấu bằng ở yêu cầu là dấu cộng.
1. Có: \(x+y=3\)
\(\Leftrightarrow\left(x+y\right)^2=3^2\)
\(\Leftrightarrow x^2+2xy+y^2=9\)
\(\Leftrightarrow x^2+y^2=9-2\cdot1=7\) (do \(xy=1\))
\(------\)
Lại có: \(x+y=3\)
\(\Leftrightarrow\left(x+y\right)^3=3^3\)
\(\Leftrightarrow x^3+y^3+3xy\left(x+y\right)=27\)
\(\Leftrightarrow x^3+y^3+3\cdot1\cdot3=27\) (do x + y = 3; xy = 1)
\(\Leftrightarrow x^3+y^3=18\)
Ta có: \(x^2+y^2=7\)
\(\Leftrightarrow\left(x^2+y^2\right)^2=7^2\)
\(\Leftrightarrow x^4+y^4+2\cdot\left(xy\right)^2=49\)
\(\Leftrightarrow x^4+y^4=49-2\cdot1=47\) (do xy = 1)

c: Ta có: x=16
nên x+1=17
Ta có: \(C=x^4-17x^3+17x^2-17x+20\)
\(=x^4-x^3\left(x+1\right)+x^2\left(x+1\right)-x\left(x+1\right)+20\)
\(=x^4-x^4-x^3+x^3+x^2-x^2-x+20\)
=20-x
=4
x,y,z>0,x+y+z=2015. MIN
A=\(\frac{x^4+y^4}{x^3+y^3}+\frac{y^4+z^4}{y^3+z^3}+\frac{z^4+x^4}{z^3+x^3}\)

Bdt phu \(\frac{a^{n+2}+b^{n+2}}{a^{n+1}+b^{n+1}}\ge\frac{a^{n+1}+b^{n+1}}{a^n+b^n}\)
cai nay ban tu chung minh nha , nhan cheo rut gon la ra
dau = khi a=b
Ap dung ta co \(\frac{x^4+y^4}{x^3+y^3}\ge\frac{x^3+y^3}{x^2+y^2}\ge\frac{x^2+y^2}{x+y}\ge\frac{x+y}{2}\)
tuong tu va suy ra \(A\ge\frac{x+y+y+z+z+x}{2}=\frac{2\left(x+y+z\right)}{2}=x+y+z=2015\)
Vay Amin = 2015 <=> x=y=z=2015/3
chuc ban hoc tot
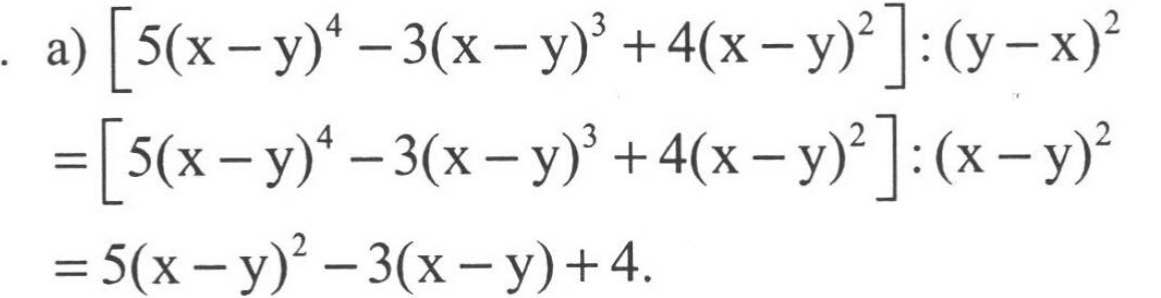
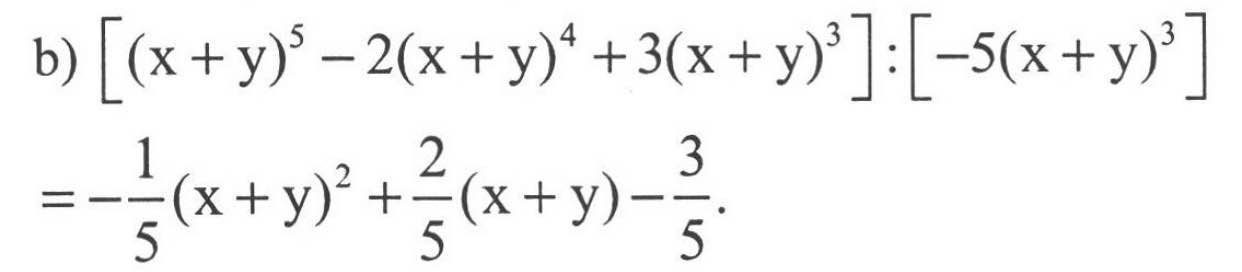
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{x}{20}=\dfrac{y}{15};\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{y}{15}=\dfrac{z}{18}\)=> \(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{18}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{10}=\dfrac{x+y-z}{20+15-18}=\dfrac{49}{17}\)
=> x= \(\dfrac{49}{17}.20\)= \(\dfrac{980}{17}\)
=> y= \(\dfrac{49}{17}.15\)= \(\dfrac{735}{17}\)
=> z= \(\dfrac{49}{17}.18=\dfrac{882}{17}\)
Đây là kết quả mình tính đc, bạn tham khảo nhé !