Tìm các cặp số nguyên (x; y) thỏa mãn: x^2-xy+3x-y=5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=\frac{x-2}{x+1}=\frac{x+1}{x+1}-\frac{3}{x+1}=1-\frac{3}{x+1}\)
P nguyên <=>3 chia hết cho x+1 <=>x+1 là Ư(3)
Mà Ư(3)={+-1;+-3}
Ta có bảng sau:
| x+1 | 1 | -1 | 3 | -3 |
| x | 0 | -2 | 2 | -4 |
Vậy x={-4;-2;0;2} thì P nguyên
p nguyên <=> x-2=x+1-3 chia hết cho x+1 => 3 chia hết cho x+1 => x+1 thuộc Ư(3) =>x+1 thuộc {-3;-1;1;3} <=> x thuộc {-4;-2;0;2}

Bài 2: Giả sử tồn tại x,y nguyên dương t/m đề, khi đó pt cho tương đương:
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x+3\right)^2+\left(2y+3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x+3=3\\2y+3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=0\\y=0\end{cases}}\)
Vậy cặp nghiệm nguyên t/m pt là (x;y) = (0;0)
Làm lại bài 2 :v (P/S: Bạn bỏ bài kia đi nhé)
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x-3\right)^2+\left(2y-3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x-3=3\\2y-3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=3\\y=3\end{cases}}\)
Vậy (x;y) = (3;3)

\(B=\frac{1}{x-y}:\frac{x+2}{2\left(x-y\right)}=\frac{1}{x-y}.\frac{2\left(x-y\right)}{x+2}=\frac{2}{x+2}\)
Để B là số nguyên
=> \(\frac{2}{x+2}\)là số nguyên
=> \(2⋮x+2\)
=> \(x+2\inƯ\left(2\right)\)
=> \(x+2\in\left\{1;-1;2;-2\right\}\)
=> \(x\in\left\{-1;-3;0;-4\right\}\)
Vậy các cặp (x ;y) thỏa mãn là (-1 ; y) ; (-3 ; y) ; (0 ; y) ; (-4 ; y) với mọi y nguyên


\(x^2-xy+y+1=0\)
\(\Leftrightarrow\left(x^2-1\right)-y\left(x-1\right)+2=0\)
\(\Leftrightarrow\left(x+1-y\right)\left(x-1\right)=-2\)
\(\Rightarrow x-1;x+1-y\inƯ\left(-2\right)=\left\{\pm1;\pm2\right\}\)
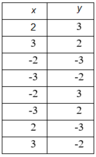
| x - 1 | 1 | -1 | 2 | -2 |
| x + 1 - y | 2 | -2 | 1 | -1 |
| x | 2 | 0 | 3 | -1 |
| y | 1 | 3 | 3 | 1 |
bảng mình xét nhầm nhé phải là như này :
| x - 1 | 1 | -1 | 2 | -2 |
| x + 1 - y | -2 | 2 | -1 | 1 |
| x | 2 | 0 | 3 | -1 |
| y | 5 | -1 | 5 | 1 |

tớ chỉ làm phần 1 thôi
1. ta có (x+5)y-x=10
=>(x+5)y-x-5=10-5
=>(x+5)y-(x+5)=5
=>(x+5)(y-1)=5
lập bảng xét giá trị của x,y \(\in Z\)
Bạn tự làm tiếp nhé -_-

x2 - xy + 3x - y = 5
\(\Leftrightarrow\) x(x - y) + x - y + 2x = 5
\(\Leftrightarrow\) (x - y)(x + 1) + 2x + 2 = 7
\(\Leftrightarrow\) (x - y)(x + 1) + 2(x + 1) = 7
\(\Leftrightarrow\) (x - y + 2)(x + 1) = 7
Vì x, y \(\in\) Z nên (x - y + 2)(x + 1) \(\in\) Z
Xét các TH:
TH1: \(\left\{{}\begin{matrix}x-y+2=7\\x+1=1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}2-y=7\\x=0\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=0\\y=-5\end{matrix}\right.\) (TM)
TH2: \(\left\{{}\begin{matrix}x-y+2=-7\\x+1=-1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}-2-y+2=-7\\x=-2\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-2\\y=7\end{matrix}\right.\) (TM)
TH3: \(\left\{{}\begin{matrix}x-y+2=1\\x+1=7\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}6-y+2=1\\x=6\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=6\\y=7\end{matrix}\right.\) (TM)
TH4: \(\left\{{}\begin{matrix}x-y+2=-1\\x+1=-7\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}-8-y+2=-1\\x=-8\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-8\\y=-5\end{matrix}\right.\) (TM)
Vậy ...
Chúc bn học tốt!