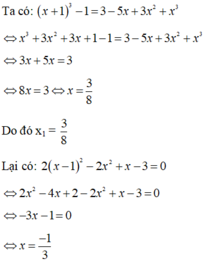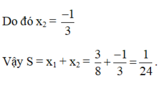Gọi x1, x2 là nghiệm của phương trình x2+ 2015x + 1 = 0; x3, x4 là nghiệm của phương trình x2+ 2016x + 1 = 0. Tính giá trị của biểu thức: ( x1 + x3)( x2 + x3)( x1 – x4)( x2 – x4)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
25 tháng 7 2021
Câu 3:
$\Delta=2015^2-4.2013.2=2011^2$
Do đó pt có 2 nghiệm:
$x_1=\frac{2015+2011}{2.2013}=1$
$x_2=\frac{2015-2011}{2.2013}=\frac{2}{2013}$
Đáp án B.
AH
Akai Haruma
Giáo viên
25 tháng 7 2021
Câu 4:
Theo định lý Viet, tổng các nghiệm của pt là:
$S=\frac{-b}{a}=\frac{-3}{1}=-3$
Đáp án B.
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{3}\\x_1x_2=-2\end{matrix}\right.\)
\(\dfrac{x_1}{x_2-1}+\dfrac{x_2}{x_1-1}=\dfrac{x_1\left(x_1-1\right)+x_2\left(x_2-1\right)}{\left(x_1-1\right)\left(x_2-1\right)}\)
\(=\dfrac{x_1^2+x_2^2-\left(x_1+x_2\right)}{x_1x_2-\left(x_1+x_2\right)+1}=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{\left(-\dfrac{5}{3}\right)^2-2.\left(-2\right)-\left(-\dfrac{5}{3}\right)}{-2-\left(-\dfrac{5}{3}\right)+1}=...\)
8 tháng 3 2022
a: Thay x=-3 vào pt, ta được:
9+6m+2m+1=0
=>8m+10=0
hay m=-5/4
b: \(\text{Δ}=\left(-2m\right)^2-4\left(2m+1\right)\)
\(=4m^2-8m-4\)
\(=4\left(m-2\right)\left(m+1\right)\)
Để phương trình có hai nghiệm thì (m-2)(m+1)>=0
=>m>=2 hoặc m<=-1
c: Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2+2x_1x_2=16\)
\(\Leftrightarrow\left(2m\right)^2=16\)
=>2m=4 hoặc 2m=-4
=>m=2(nhận) hoặc m=-2(nhận)
CM
28 tháng 5 2018
Đáp án B
P T ⇔ 2 2 x 2 − 5 2 x + 2 = 0 ⇔ 2 x = 2 2 x = 1 2 ⇔ x = 1 x = − 1 ⇒ x 1 = − 1 x 2 = 1 ⇒ x 2 − x 1 = 2.