Rút gọn các biểu thức: x^2+4/x^2+2x+4/x+2, với x ko=0; x ko=-2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: P = x − x + 2 ( x + 1 ) ( x − 2 ) − x x ( x − 2 ) : 1 − x 2 − x = x − x + 2 − x ( x + 1 ) ( x + 1 ) ( x − 2 ) . 2 − x 1 − x = 2 − 2 x ( x + 1 ) ( x − 1 ) = 2 ( 1 − x ) ( x + 1 ) ( x − 1 ) = − 2 x + 1

Lời giải:
1.
$M=(x^2+6x+9)+(x^2-9)-2(x^2-2x-8)$
$=x^2+6x+9+x^2-9-2x^2+4x+16=(x^2+x^2-2x^2)+(6x+4x)+(9-9+16)$
$=10x+16=5(2x+1)+11=5.0+11=11$
2.
$V=(9x^2+24x+16)-(x^2-16)-10x=9x^2+24x+16-x^2+16-10x$
$=(9x^2-x^2)+(24x-10x)+(16+16)=8x^2+14x+32$
$=8(\frac{-1}{10})^2+14.\frac{-1}{10}+32=\frac{767}{25}$
3.
$P=(x^2+2x+1)-(4x^2-4x+1)+3(x^2-4)$
$=x^2+2x+1-4x^2+4x-1+3x^2-12$
$=(x^2-4x^2+3x^2)+(2x+4x)+(1-1-12)$
$=6x-12=6.1-12=-6$
4.
$Q=(x^2-9)+(x^2-4x+4)-2x^2+8x$
$=x^2-9+x^2-4x+4-2x^2+8x$
$=(x^2+x^2-2x^2)+(-4x+8x)-9+4$
$=4x-5=4(-1)-5=-9$

\(\dfrac{2\left(2-\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}+\dfrac{2\sqrt{x}\left(2+\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}-\dfrac{2x}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{4-2\sqrt{x}+4\sqrt{x}+2x-2x}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{4-2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{2\left(2-\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{2}{2+\sqrt{x}}\)

Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề và hỗ trợ bạn tốt hơn nhé.

\(B=\dfrac{1-4\sin^2x\cdot\cos^2x}{\sin^2x+2\sin x\cdot\cos x+\cos^2}+2\sin x\cdot\cos x\\ B=\dfrac{1-4\sin^2x\cdot\cos^2x}{2\sin x\cdot\cos x}+2\sin x\cdot\cos x\\ B=\dfrac{1-4\sin^2x\cdot\cos^2x+4\sin^2x\cdot\cos^2x}{2\sin x\cdot\cos x}=\dfrac{1}{2\sin x\cdot\cos x}\)
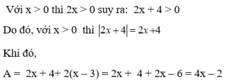
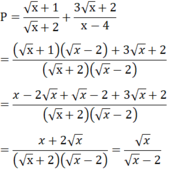
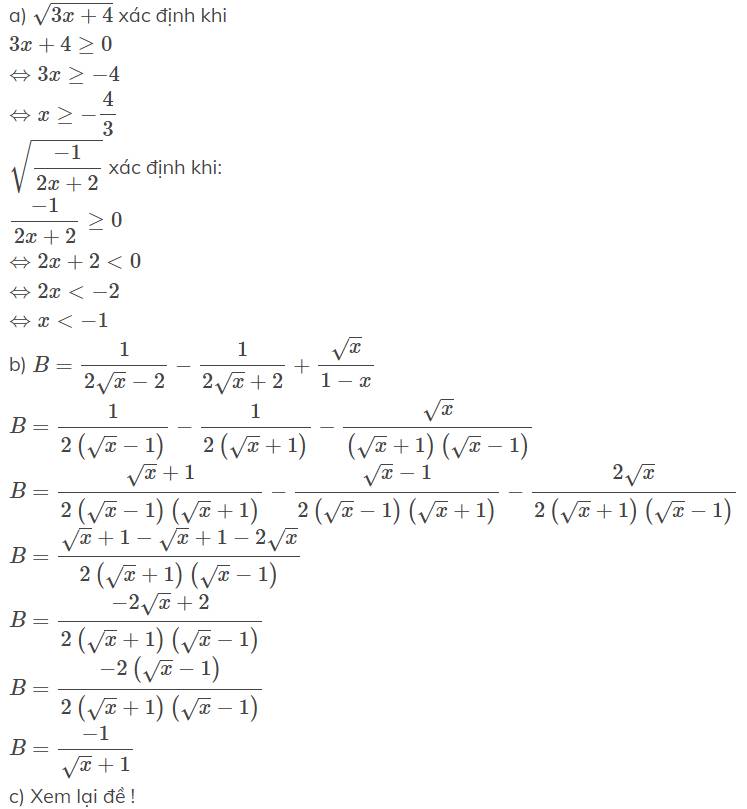
\(=\dfrac{x^2+4}{x\left(x+2\right)}+\dfrac{4}{x+2}=\dfrac{x^2+4x+4}{x\left(x+2\right)}=\dfrac{x+2}{x}\)
\(\dfrac{x^2+4}{x^2+2x}+\dfrac{4}{x+2}=\dfrac{x^2+4+4x}{x\left(x+2\right)}=\dfrac{\left(x+2\right)^2}{x\left(x+2\right)}=\dfrac{x+2}{x}\)