Giúp mình với
Giả sử hàm số y=f(x) liên tục, dương trên (0;+vô cùng) thỏa mãn f(1)=1 và \(f^2\left(x\right)=x^3f^'\left(x\right);\forall x\in\left(0;+vocung\right)\) . Giá trị f(2) thuộc khoảng nào dưới đây
A(0;1) B(2;4) C(1;2) D(6;7)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 7 2017
Đáp án A
Phương pháp : Sử dụng phương pháp đổi biến, đặt x = a – t.
Cách giải : Đặt x = a – t => dx = –dt. Đổi cận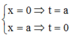 
=> 
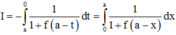
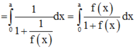
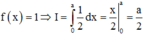
CM
4 tháng 1 2017
Chọn A.
Từ giả thiết, suy ra f a - x = 1 f x
Đặt t=a-x suy ra dt=-dx . Đổi cận: x = 0 → t = a x = a → t = 0
Khi đó
.
.
.
.
CM
9 tháng 8 2018
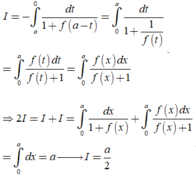
Đáp án D
Ta có f x = f ' x 3 x + 1
⇔ f ' x f x = 1 3 x + 1 ⇔ ∫ f ' x f x d x = ∫ d x 3 x + 1
⇔ ∫ a f x f x = ∫ 3 x + 1 − 1 2 d x
⇔ ln f x = 2 3 3 x + 1 + C ⇔ f x = e 2 3 3 x + 1 + C
Mặt khác f 1 = 1
suy ra 1 = e 4 3 + C
⇔ C = − 4 3 ⇒ f 5 ≈ 3 , 793
Kiến thức bài này nằm ở giữa gần cuối chương trình lớp 12, lớp 11 ko thể giải được đâu bạn
\(f^2\left(x\right)=x^3f'\left(x\right)\Rightarrow\frac{f'\left(x\right)}{f^2\left(x\right)}=\frac{1}{x^3}\)
Lấy nguyên hàm 2 vế:
\(\int\frac{f'\left(x\right)}{f^2\left(x\right)}dx=\int\frac{dx}{x^3}\Leftrightarrow\frac{-1}{f\left(x\right)}=-\frac{1}{2x^2}+C\)
Do \(f\left(1\right)=1\Rightarrow\frac{-1}{1}=-\frac{1}{2}+C\Rightarrow C=-\frac{1}{2}\)
\(\Rightarrow-\frac{1}{f\left(x\right)}=-\frac{1}{2x^2}-\frac{1}{2}\Rightarrow\frac{1}{f\left(x\right)}=\frac{1}{2x^2}+\frac{1}{2}\Rightarrow f\left(x\right)=\frac{2x^2}{x^2+1}\)
\(\Rightarrow f\left(2\right)=\frac{8}{5}\) \(\Rightarrow\) đáp án C