Với m,n∈Zm,n∈Z ; sao cho \(\dfrac{1}{m}\)+\(\dfrac{n}{6}\)=12. Số cặp giá trị (m;n)(m;n) thỏa mãn là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : m.n( m2.n2 )
= m.n [( m2 - 1 ) - ( n2 - 1)]
= m( m2 - 1 )n - mn( n2 - 1 )
= ( m - 1 )m( m + 1 )n - m( n - 1 )n( n + 1 )
Ta thấy: * ( m - 1) ; m và ( m + 1) là ba số nguyên liên tiếp
=> ( m - 1 )m( m + 1 ) chia hết cho 6
=> ( m - 1 )m ( m + 1 )n chia hết cho 6 (1)
* ( n - 1) ; n ; ( n + 1 ) là ba số nguyên liên tiếp
=> ( n - 1)n( n + 1 ) chia hết cho 6
=> m( n - 1 )n( n + 1 ) chia hết cho 6 (2)
Từ (1) và (2) suy ra : ( m - 1)m( m + 1)n - m( n - 1)n( n + 1 ) chia hết cho 6
Vậy m.n( m2.n2 ) chia hết cho 6 (đpcm)
Hok tốt !
Em kiểm tra lại đề và có thể tham khảo 1 cách giải ( lớp 7 có thể hiểu):
Câu hỏi của Luong Ngoc Quynh Nhu - Toán lớp 8 - Học toán với OnlineMath

a) Để M nhận giá trị nguyên thì \(6n-1⋮3n+2\)
\(\Leftrightarrow6n+4-5⋮3n+2\)
\(\Leftrightarrow2\left(3n+2\right)-5⋮3n+2\)
Do \(2\left(3n+2\right)⋮3n+2\) \(\Rightarrow5⋮3n+2\)
Do 3n+2 chia 3 dư 2, mà 5 chia hết cho 3n+2
\(\Rightarrow3n+2\in\left\{-1;5\right\}\)
\(\Leftrightarrow n\in\left\{-1;1\right\}\)
Vậy: n=-1 hoặc n=1

\(A=\frac{2n+3}{n}=2+\frac{3}{n}\)
a) A là phân số <=> n khác Ư(3) <=> n khác (+-1; +-3)
b) A thuộc Z <=> n thuộc Ư(3) <=> n thuộc (+-1; +-3)

Chọn D
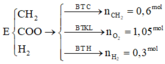
Dồn chất:
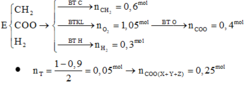
→ B T K L m = 26 , 6 + 0 , 8 . 40 - 0 , 05 . 92 - 18 . 0 , 25 2 = 24 , 75 g a m
·

Ta có:
\(n_{hh}=\frac{5,6}{22,4}=0,25\left(mol\right)\)
Gọi \(\left\{{}\begin{matrix}n_{O2}:x\left(mol\right)\\n_{Cl2}:y\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow x+y=0,25\left(1\right)\)
\(\Rightarrow\frac{32x+71y}{x+y}=58\Rightarrow58x+58y=32x+71y\)
\(\Rightarrow26x=13y\) hay \(26x-13y=0\left(2\right)\)
\(\Rightarrow\frac{x}{y}=\frac{1}{2}\)
\(\left\{{}\begin{matrix}\%V_{O2}=\frac{1}{3}.100\%=33,33\%\\\%V_{Cl2}=100\%-33,33\%=66,67\%\end{matrix}\right.\)
b) \(\left(1\right)+\left(2\right)\Rightarrow\left\{{}\begin{matrix}x+y=0,25\\26x-13y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\frac{1}{12}\left(mol\right)\\y=\frac{1}{6}\left(mol\right)\end{matrix}\right.\)
Lời giải:
$\frac{1}{m}+\frac{n}{6}=12$
$\Rightarrow 6+mn=72m$
$\Leftrightarrow 6=m(72-n)$
Vì $m,72-n$ là số nguyên với mọi $m,n$ nguyên nên xét các TH:
$m=1; 72-n=6\Rightarrow (m,n)=(1,66)$
$m=6, 72-n=1\Rightarrow (m,n)=(6,71)$
$m=-1, 72-n=-6\Rightarrow (m,n)=(-1,78)$
$m=-6, 72-n=-1\Rightarrow (m,n)=(-6,73)$
$m=-2, 72-n=-3\Rightarrow (m,n)=(-2,75)$
$m=-3, 72-n=-2\Rightarrow (m,n)=(-3,74)$
$m=2, 72-n=3\Rightarrow (m,n)=(2,69)$
$m=3, 72-n=2\Rightarrow (m,n)=(3,70)$