Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ta có qua 2 điểm ta vẽ được 1 đường thẳng
3điểm ta vẽ được 2đương thẳng
n điểm ta vẽ được n(n-1):2 đường thẳng
- Nếu trong n điểm không có 3 điểm nào thẳng hàng thì số đường thẳng kẻ được là \(\dfrac{n\left(n-1\right)}{2}\) đường.
- Số đường thẳng bị giảm nếu n điểm trong đó không có 3 điểm nào thẳng hàng trở thành n điểm thẳng hàng là: \(\dfrac{n\left(n-1\right)}{2}-1\) đường.
- Số đường thẳng tạo bởi 100 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng là: \(\dfrac{100.99}{2}=4950\) đường.
- Theo đề bài ta có: \(4950-\left(\dfrac{n\left(n-1\right)}{2}-1\right)=4915\)
\(\Leftrightarrow n\left(n-1\right)=72\)
\(\Leftrightarrow n^2-n-72=0\)
Giải phương trình trên ta được \(n=9\left(n\right)\) hay \(n=-8\) (loại)
Vậy n=9.
Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d1 và hai đỉnh thuộc d2. Loại này có 
tam giác.
Loại 2: Tam giác có một đỉnh thuộc d2 và hai đỉnh thuộc d1. Loại này có 
tam giác.
Theo bài ra ta có: 
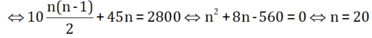
Chọn A.
Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d 1 và hai đỉnh thuộc d 2 .
Loại này có C 10 1 . C n 2 tam giác.
Loại 2: Tam giác có một đỉnh thuộc d 2 và hai đỉnh thuộc d 1 .
Loại này có C 10 2 . C n 1 tam giác.
Theo bài ra ta có: C 10 1 . C n 2 + C 10 2 . C n 1 = 2800
⇔ 10 n ( n − 1 ) 2 + 45 n = 2800 ⇔ n 2 + 8 n − 560 = 0 ⇔ n = 20
Chọn đáp án D
Gọi n điểm đã cho là: \(A_1;A_2;A_3;...;A_n\); n\(\ge\)2.
Vì không có 3 điểm nào thẳng hàng nên :
+) Nối \(A_1\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
+) Nối \(A_2\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
+) Nối \(A_3\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
...
+) Nối \(A_3\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
Như chúng ta có: n ( n - 1) đường thẳng
Tuy nhiên mỗi đường thẳng được tính 2 lần ( VD như nối \(A_1\)với \(A_2\)ta có đường thẳng \(A_1\)\(A_2\); còn nối \(A_2\)với \(A_1\)ta có đường thẳng \(A_2\)\(A_1\); và 2 đường thẳng \(A_1\)\(A_2\); \(A_2\)\(A_1\) trùng nhau )
=> Do đó số đường thẳng phân biệt là: n ( n - 1) : 2.
Ta thấy: Trong n điểm phân biệt cho trước, cứ qua 1 điểm ta vẽ được n - 1 đường thẳng. Vậy qua n điểm ta vẽ được n(n - 1) đoạn thẳng.
Nhưng nếu tính vậy thì mỗi đường thẳng sẽ bị tính đi tính lại 2 lần
Vậy số đoạn thẳng phân biệt được tạo ra từ n điểm phân biệt trên là: \(\frac{n\left(n-1\right)}{2}\)(đường thẳng)
Đáp án là C
Số đoạn thẳng tạo thành từ n điểm phân biệt trong đó không có ba điểm nào thẳng hàng là: n(n - 1)/2 (n ≥ 2; n ∈ N)
Theo đề bài có 28 đoạn thẳng được tạo thành nên ta có: n(n - 1)/2 = 28 ⇒ n(n - 1) = 56 = 8.7
Nhận thấy (n - 1) và n là hai số tự nhiên liên tiếp, suy ra n = 8.