1. Cho Tam giác ABC; gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh: Tam giác ABC = Tam giác DCM
b) Chứng minh: AB song song với CD
c) Kẻ BH vuông góc với AM ( H thuộc AM ), CK vuông góc với DM ( K thuộc DM ), cho biết MK = 1,5 cm. Tính độ dài đoạn thẳng HK.
2. Cho 3 số thực a, b, c thỏa mãn: \(\frac{a}{2015}\)= \(\frac{b}{2016}\)= \(\frac{c}{2017}\)
Chứng minh rằng: 4(a - b)(b - c) = (c - a)2

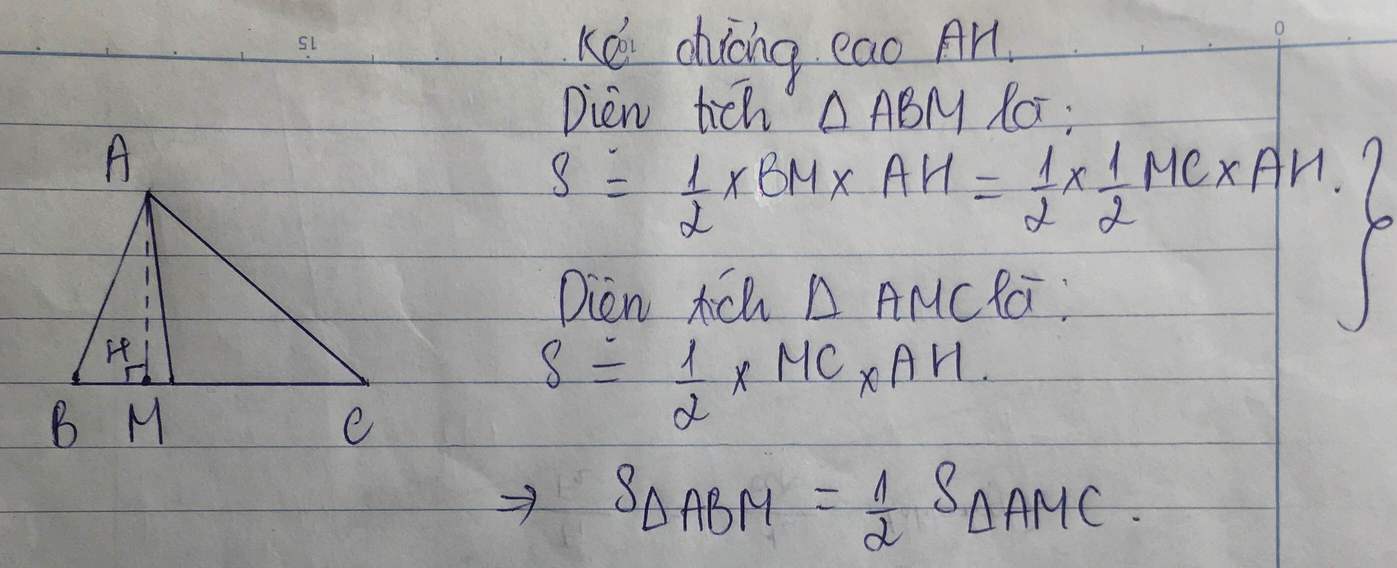

Sửa lại đề câu a là chứng minh \(\Delta\)ABC = \(\Delta\)DCM thành chứng minh \(\Delta\)ABM = \(\Delta\)DCM
a) Xét \(\Delta\)ABM và \(\Delta\)DCM có:
AM = DM (gt)
\(\widehat{AMB}\) = \(\widehat{DMC}\)
BM = CM (suy từ gt)
=> \(\Delta\)ABM = \(\Delta\)DCM (c.g.c)
b) Vì \(\Delta\)ABM = \(\Delta\)DCM (theo câu a)
nên \(\widehat{BAM}\) = \(\widehat{CDM}\) (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong nên AB // CD
c) .............
Câu 2:
Đặt \(\frac{a}{2015}\) = \(\frac{b}{2016}\) = \(\frac{c}{2017}\) = k
=> a = 2015k; b = 2016k và c = 2017k
Xét hiệu:
4 (2015k - 2016k)(2016k - 2017k) - (2017k - 2015k)2
= 4 (-k) (-k) - (2k)2
= 4k2 - 4k2
= 0
Do đó 4(a - b)(b - c) = (c - a)2. \(\rightarrow\) đpcm.