Hình chóp SABC có SA ⊥ (ABC). Hạ AE ⊥ BC, biết AE = a 2 ; góc giữa (ABC) và (ABC) bằng 60º. Tính khoảng cách h từ A tới mặt phẳng (SBC).
A. h = a 3 2
B. h = a 3 2
C. h = a 3
D. h = a 2 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 6 2017
Đáp án là B.
V S . A B C = 1 3 S A . S Δ A B C = 1 3 . a 3 . a 2 3 4 = a 3 4 .
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 8 2021
\(AC=\sqrt{BC^2-AB^2}=\dfrac{a\sqrt{3}}{4}\)
Gọi H là hình chiếu vuông góc của S lên đáy
Do \(SA=SB=SC\Rightarrow HA=HB=HC\Rightarrow H\) là tâm đường tròn ngoại tiếp ABC
Mà ABC vuông tại A \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow BH=\dfrac{1}{2}BC=\dfrac{a}{2}\)
\(\Rightarrow SH=\sqrt{SB^2-BH^2}=\dfrac{a\sqrt{15}}{2}\)
\(V=\dfrac{1}{3}SH.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.\dfrac{a\sqrt{15}}{2}.\dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a\sqrt{3}}{4}=\dfrac{a^3\sqrt{5}}{32}\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 7 2021
Ủa cái a căn 2(6) phải dịch thế nào cho đúng?
\(AC=\sqrt{BC^2-AB^2}=a\sqrt{3}\)
\(V=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.2a\sqrt{6}.\dfrac{1}{2}.a.a\sqrt{3}=a^3\sqrt{2}\)
18 tháng 11 2021
Cho hình chop SABC, có đáy là ABC là tam giác vuông tại B, có độ dài các cạch AB=6,BC=8,SA=10 vuông góc với mặt đáy Tính thể tích khối chóp SABC
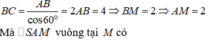
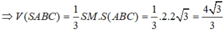
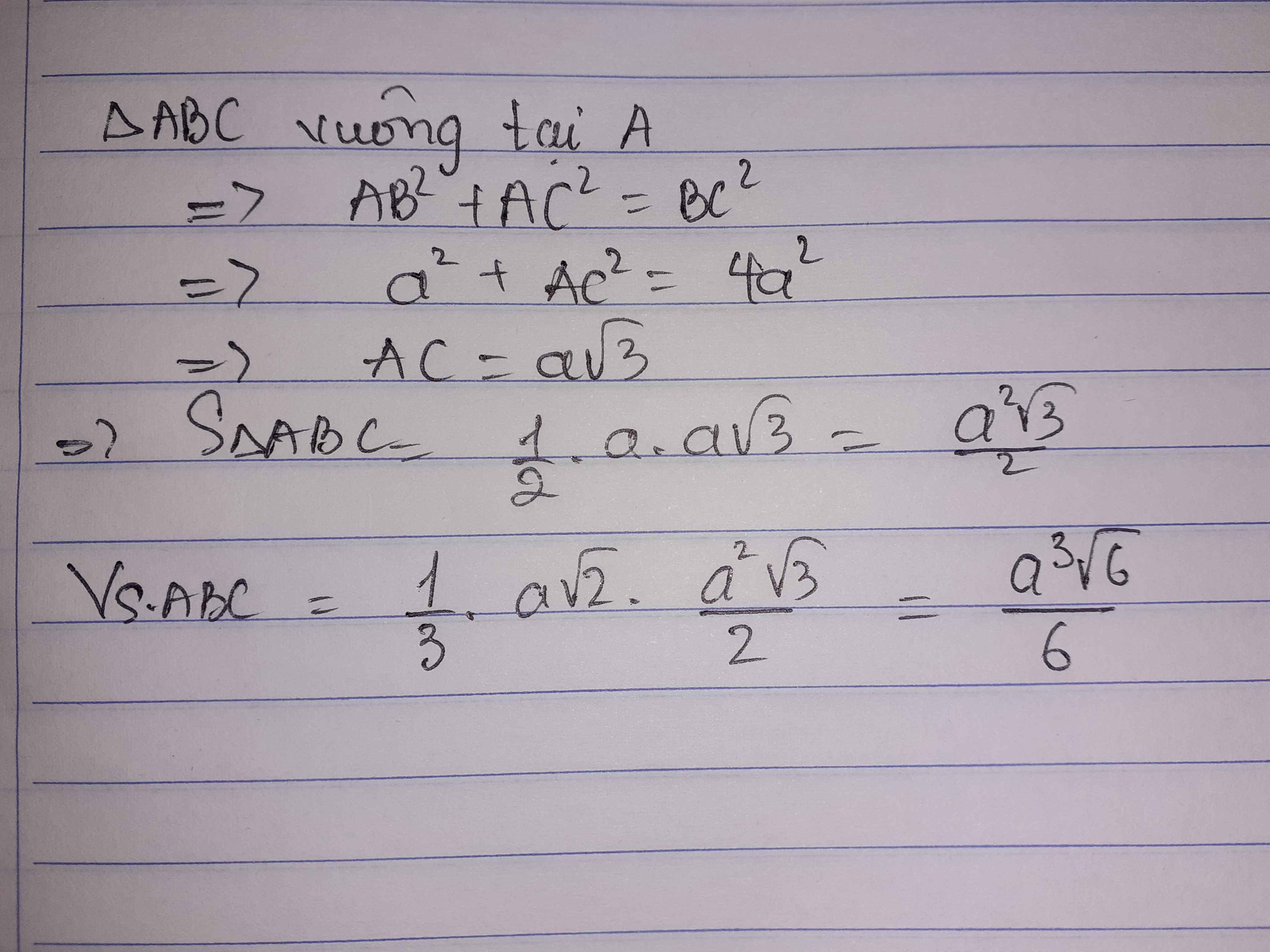
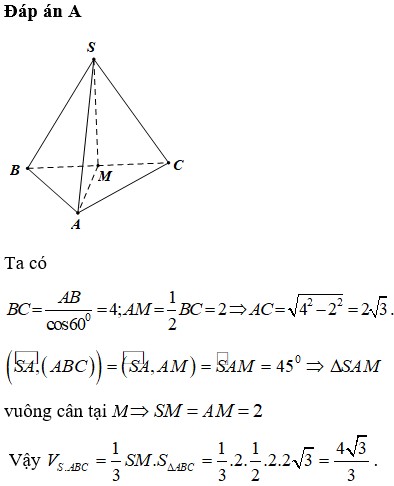
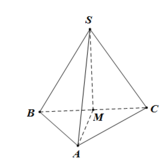
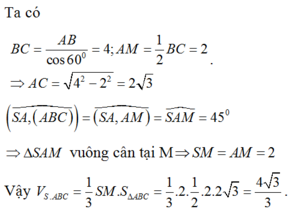
Đáp án A