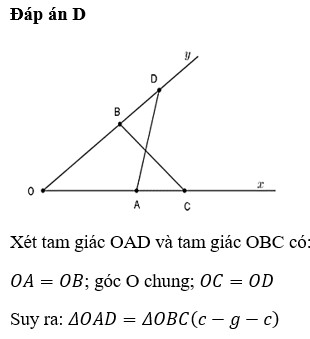
Cho góc xOy khác góc bẹt. Trên tia Õ lấy điểm A và D ( A nằm giữa O và D ) trên tia Oy lấy điểm B và C ( B nằm giữa tia Oy lấy điểm B và C ( B nằm giữa O và C ) sao cho OA = OB ; góc OAC = góc OAB, AC cắt BD tại I. Chứng minh IC = ID
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 3 2020
Câu hỏi của nguyenvandat - Toán lớp 7 - Học toán với OnlineMath
9 tháng 12 2021
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
AH
Akai Haruma
Giáo viên
30 tháng 12 2020
Lời giải:
a) Xét tam giác AOD và COB có:
\(AO=CO\) (giả thiết)
\(OD=OB\) (giả thiết)
\(\widehat{O}\) chung
\(\Rightarrow \triangle AOD=\triangle COB (c.g.c)\) (đpcm)
b)
Vì \(OA=OC; OB=OD\Rightarrow OB-OA=OD-OC\) hay \(AB=CD\)
\(OB=OD\) nên tam giác OBD cân tại O. Do đó \(\widehat{OBD}=\widehat{ODB}\) hay \(\widehat{ABD}=\widehat{CDB}\)
Xét tam giác ABD và CDB có:
\(BD\) chung
\(\widehat{ABD}=\widehat{CDB}\) (cmt)
\(AB=CD\) (cmt)
Do đó $\triangle ABD=\triangle CDB$ (c.g.c)
Ta có đpcm.
14 tháng 2 2020
a) Xét ▲OAD và ▲OBC có :
OA = OB ( gt )
góc COD chung
OC = OD ( gt )
=> ▲OAD = ▲OBC ( c-g-c )
=> đpcm
b) Gọi giao điểm của BC và AD là M
Vì ▲OAD = ▲OBC ( c/m trên )
=> góc OCB = góc ODA ( 2 góc tương ứng )
Xét ▲ACM có góc MAC + góc ACM + góc CMA = 1800
Xét ▲BMD có góc BMD + góc MDB + góc DBM = 1800
Mà góc OCB = góc ODA ( c/m trên ) và góc CMA = góc BMD ( đối đỉnh )
=> góc CAM = góc MBD ( đpcm )
TT
7 tháng 2 2021
a/ Xét t/g OAD và t/g OBC cos
AO = OB
\(\widehat{xOy}\) : chung
OD = OC
=> t/g OAD = t/g OBC
=> AD = BC
b/ Không rõ đề.
c/ Có
OC = ODOA = OB
=> AC = BD
Có \(\widehat{OAD}=\widehat{OBE}\) (do t/g OAD = t/g OBC)
=> \(180^o-\widehat{OAD}=180^o-\widehat{OBE}\)
=> \(\widehat{CAD}=\widehat{CBD}\)
Xét t/g AEC và t/g BED có
\(\widehat{CAD}=\widehat{CBD}\)
AC = BD\(\widehat{OCB}=\widehat{ODA}\)
=> t/g AEC = t/g BED (g.c.g)
=> AE = BE
Xét t/g OAE và t/g OBE có
OA = OB
AE = BEOE : chung
=> t/g OAE = t/g OBE
=> ^xOE = ^yOe
=> OE là pg góc xOy