Cho tam giác ABC cân tại A; góc B = 75 độ , kẻ CH vuông góc AB . C/minh: CH = \(\dfrac{AB}{2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 4 2018
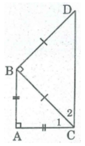
Vì ΔABC vuông cân tại A nên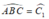 
Lại có: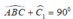 
( tính chất tam giác vuông).
Suy ra: ∠ C 1 = 45 0
Vì
∆
BCD vuông cân tại B nên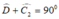 
Lại có: 
( tính chất tam giác vuông).
Suy ra: ∠ C 2 = 45 0
∠ (ACD) = ∠ C 1 + ∠ C 2 = 45 0 + 45 0 = 90 0
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB //CD
Vậy tứ giác ABCD là hình thang vuông.
2 tháng 9 2023
ΔBDC vuông cân tại B
=>góc BCD=góc BDC=45 độ
ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc ABC=góc DCB
mà hai góc này ở vị trí so le trong
nên AB//DC
mà AB vuông góc AC
nên DC vuông góc AC
Xét tứ giác ABDC có
AB//DC
góc CAB=90 độ
Do đó: ABDC là hình thang vuông
PL
21 tháng 6 2016
Vì tam giác ABC vuông cân tại A (gt) nên góc ABC = góc ACB = 90 : 2 = 45 độ
Vì tam giác BCD vuông cân tại B (gt) nên góc BDC = góc BCD = 90 : 2 = 45 độ
Ta có: góc ACB + góc BCD = góc ACD = 45 độ + 45 độ = 90 độ
hay AC vuông góc DC. (1)
Vì tam giác ABC vuông cân tại A (gt) nên AC vuông góc AB (2)
Từ (1) và (2) suy ra DC // AB
Do đó tứ giác ABCD là hình thang.
ACHB
Ta có : \(\widehat{B}=\widehat{ACB}\) ( \(\Delta\) cân tại A )
==> \(\widehat{ACB}=75\) độ
Tam giác HCB vuông tại H có: \(\widehat{B}+\widehat{HCB}=90\) độ
75 + \(\widehat{HCB}\) = 90 độ
\(\widehat{HCB}\) = 15 độ
Mà \(\widehat{ACB}=\widehat{HCB}+\widehat{ECD}\)
75 = 15 + \(\widehat{ECD}\)
==> \(\widehat{ECD}\) = 60độ
Tam giác AHC có: \(\widehat{H}=90\) độ (gt)
\(\widehat{ECD=}60\) độ (cmt)
==> Tam giác AHC là nửa tam giác đều.
==> 2CH = AC
Mà AC = AB ( \(\Delta\) ABC cân tại A )
==> 2CH = AB hay \(CH=\dfrac{AB}{2}\) (đpcm)
Nếu còn gì thắc mắc thì vào phần bình luận nhé!
CHÚC BẠN HỌC TỐT ***